[Python] 머신러닝 완벽가이드 - 06. 차원축소[LDA]
Updated:
파이썬 머신러닝 완벽가이드 교재를 토대로 공부한 내용입니다.
실습과정에서 필요에 따라 내용의 누락 및 추가, 수정사항이 있습니다.
기본 세팅
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
mpl.rc('font', family='NanumGothic') # 폰트 설정
mpl.rc('axes', unicode_minus=False) # 유니코드에서 음수 부호 설정
# 차트 스타일 설정
sns.set(font="NanumGothic", rc={"axes.unicode_minus":False}, style='darkgrid')
plt.rc("figure", figsize=(10,8))
warnings.filterwarnings("ignore")
3 LDA(Linear Discriminant Analysis)
LDA
LDA는 선형 판별 분석법으로 불리며 PCA와 매우 유사하다.
다만 LDA는 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소한다.
-
PCA는 입력 데이터의 변동성이 가장 큰 축을 찾는다.
-
LDA는 입력 데이터의 결정 값 클래스를 최대한 분리할 수 있는 축을 찾는다.
LDA는 클래스 분리를 최대화 하는 축을 찾기 위해 클래스 간 분산은 최대화하고 클래스 내 분산은 최소화한다.
PCA가 공분산 행렬을 사용한 반면 LDA는 클래스 간 분산, 클래스 내 분산 행렬을 사용하는 것이 가장 큰 차이점이다.
LDA 수행과정
-
클래스 내부와 클래스 간 분산 행렬을 계산한다. 두 행렬은 입력 데이터의 결정값 클래스별로 개별 피처의 평균 벡터를 기반으로 구한다.
-
클래스 내부 분산 행렬을 $S_{W}$, 클래스 간 분산을 $S_{B}$라 하면 다음과 같이 표현 가능하다.
-
고유값이 가장 큰 순으로 K개(LDA의 변환 차수)만큼 고유벡터를 추출한다.
-
고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터를 변환한다.
3.1 IRIS 데이터
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
iris = load_iris()
# 피처 스케일링
iris_scaled = StandardScaler().fit_transform(iris.data)
- 선행 작업으로 IRIS 데이터의 피처를 스케일링 하였다.
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# 변환할 차원 수 입력
lda = LinearDiscriminantAnalysis(n_components=2)
# 학습
lda.fit(iris_scaled, iris.target)
iris_lda = lda.transform(iris_scaled)
print(f"스케일 데이터 shape: {iris_scaled.shape}")
print(f"LDA 데이터 shape: {iris_lda.shape}")
스케일 데이터 shape: (150, 4)
LDA 데이터 shape: (150, 2)
-
LDA를 이용해 기존 4차원(4개 피처)에서 2차원으로 변환 하였다.
-
비지도학습인 PCA와는 다르게 LDA는 지도학습으로서 클래스의 결정 값 즉, target이 꼭 필요하다.
# LDA 데이터 프레임 생성
lda_columns=['lda_component_1','lda_component_2']
iris_df_lda = pd.DataFrame(iris_lda, columns = lda_columns)
iris_df_lda['target'] = iris.target
iris_df_lda.head(3)
| lda_component_1 | lda_component_2 | target | |
|---|---|---|---|
| 0 | 8.061800 | 0.300421 | 0 |
| 1 | 7.128688 | -0.786660 | 0 |
| 2 | 7.489828 | -0.265384 | 0 |
markers = ["^", "s", "o"]
# 0:setosa, 1:versicolor, 2:virginica
for i, marker in enumerate(markers):
x_axis_data = iris_df_lda[iris_df_lda['target']==i]['lda_component_1']
y_axis_data = iris_df_lda[iris_df_lda['target']==i]['lda_component_2']
plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i])
plt.legend(loc="upper right")
plt.xlabel('lda_component_1')
plt.ylabel('lda_component_2')
plt.show()
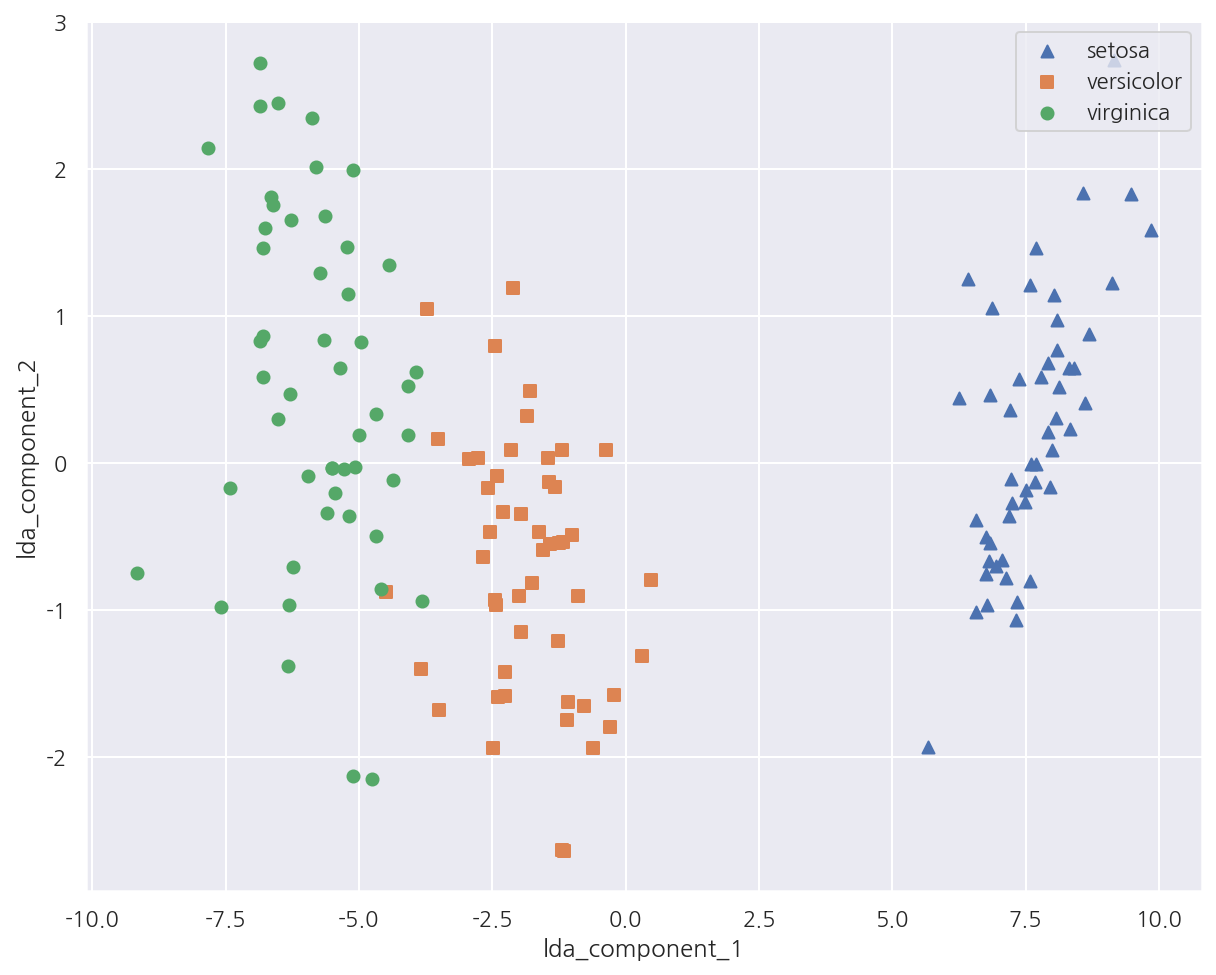
-
LDA 변환 후 2개의 속성(피처)로 붓꽃 종류를 시각화 하였다.
-
모든 붓꽃 종류가 lda_component_1 축을 기반으로 비교적 잘 구분되었다.

Leave a comment