[Python] 머신러닝 완벽가이드 - 06. 차원축소[SVD]
Updated:
파이썬 머신러닝 완벽가이드 교재를 토대로 공부한 내용입니다.
실습과정에서 필요에 따라 내용의 누락 및 추가, 수정사항이 있습니다.
기본 세팅
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
mpl.rc('font', family='NanumGothic') # 폰트 설정
mpl.rc('axes', unicode_minus=False) # 유니코드에서 음수 부호 설정
# 차트 스타일 설정
sns.set(font="NanumGothic", rc={"axes.unicode_minus":False}, style='darkgrid')
plt.rc("figure", figsize=(10,8))
warnings.filterwarnings("ignore")
4.SVD(Singular Value Decomposition)
SVD
SVD는 특이값 분해라 불리며, PCA와 유사한 행렬 분해 기법을 사용한다.
PCA는 정방행렬만을 고유벡터로 분해할 수 있지만, SVD는 정방행렬이 아니어도 적용 가능하다.
SVD는 m x n 행렬 $A$를 다음과 같이 분해한다.
\[A = U\Sigma V^{T}\]-
$U$: m x m 행렬로 속한 벡터는 특이벡터(Singular Vector)로 서로 직교한다.
-
$\Sigma$: m x n 행렬로 대각원소(행렬 $A$의 특이값)만 0이 아니고 나머지 값은 0이다.
-
$V^{T}$: n x n 행렬로 속한 벡터는 특이벡터(Singular Vector)로 서로 직교한다.
위 과정을 Full SVD라 하며, 일반적으로는 이를 축약해서 사용한다.
Compact SVD
Compact SVD는 Full SVD를 축약한 방법 중 하나로 다음과 같이 분해한다.
-
$\Sigma$의 비대각인 부분과 특이값이 0인 부분을 제거한다.
-
이에 대응하는 $U$와 $V$의 원소도 함께 제거해 차원을 줄인 형태로 SVD를 적용한다.
-
즉, $U$: m x p, $\Sigma$: p x p, $V^{T}$: p x n 과 같이 차원이 줄어든다.
Truncated SVD
Truncated SVD 역시 Full SVD를 축약한 방법으로 $\Sigma$의 대각원소 중에 상위 몇 개만 추출하는 방식이다.
Compact SVD보다도 더욱 차원을 줄인 방식으로 과정 자체는 Compact SVD와 차이가 없다.
인위적으로 더 작은 차원으로 분해하기 때문에 원본 행렬 복구가 불가능하다.
4.1 Full SVD
# a: 4 X 4
np.random.seed(121)
a = np.random.randn(4,4)
print(np.round(a, 3))
[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]
- 행렬이 선형독립이게끔 4 x 4 랜덤행렬을 생성하였다.
numpy 패키지
# Full SVD
U, Sigma, Vt = np.linalg.svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print("-"*35)
print('U matrix:\n',np.round(U, 3))
print("-"*35)
print('Sigma Value:\n',np.round(Sigma, 3))
print("-"*35)
print('V transpose matrix:\n',np.round(Vt, 3))
(4, 4) (4,) (4, 4)
-----------------------------------
U matrix:
[[-0.079 -0.318 0.867 0.376]
[ 0.383 0.787 0.12 0.469]
[ 0.656 0.022 0.357 -0.664]
[ 0.645 -0.529 -0.328 0.444]]
-----------------------------------
Sigma Value:
[3.423 2.023 0.463 0.079]
-----------------------------------
V transpose matrix:
[[ 0.041 0.224 0.786 -0.574]
[-0.2 0.562 0.37 0.712]
[-0.778 0.395 -0.333 -0.357]
[-0.593 -0.692 0.366 0.189]]
-
np.linalg.svd()에 행렬을 입력하면 $U$, $\Sigma$, $V^{T}$를 반환해준다. -
$\Sigma$의 경우 대각원소 값만 표현하여 1차원 행렬로 반환된다.
scipy 패키지
import scipy
# Full SVD
U, Sigma, Vt = scipy.linalg.svd(a, full_matrices=True)
print(U.shape, Sigma.shape, Vt.shape)
print("-"*35)
print('U matrix:\n',np.round(U, 3))
print("-"*35)
print('Sigma Value:\n',np.round(Sigma, 3))
print("-"*35)
print('V transpose matrix:\n',np.round(Vt, 3))
(4, 4) (4,) (4, 4)
-----------------------------------
U matrix:
[[-0.079 -0.318 0.867 0.376]
[ 0.383 0.787 0.12 0.469]
[ 0.656 0.022 0.357 -0.664]
[ 0.645 -0.529 -0.328 0.444]]
-----------------------------------
Sigma Value:
[3.423 2.023 0.463 0.079]
-----------------------------------
V transpose matrix:
[[ 0.041 0.224 0.786 -0.574]
[-0.2 0.562 0.37 0.712]
[-0.778 0.395 -0.333 -0.357]
[-0.593 -0.692 0.366 0.189]]
numpy패키지 뿐 아니라scipy패키지의scipy.linalg.svd()를 이용하여 Full SVD 수행이 가능하다.
# Sigma 행렬 대칭행렬로 변환
Sigma_mat = np.diag(Sigma)
# a 행렬 되돌리기
a_ = U @ Sigma_mat @ Vt
print(np.round(a_, 3))
[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]
- $\Sigma$를 2차원으로 바꿔준 후 행렬을 곱하여 원래의 행렬이 만들어짐을 확인하였다.
a[2] = a[0] + a[1]
a[3] = a[0]
print(np.round(a,3))
[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.542 0.899 1.041 -0.073]
[-0.212 -0.285 -0.574 -0.44 ]]
- 행렬이 선형종속이게끔 세 번째 행을 첫 번째 행 + 두 번째 행, 네 번째 행은 첫 번째 행과 같게 만든다.
# Full SVD
U, Sigma, Vt = np.linalg.svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print("-"*35)
print('U matrix:\n',np.round(U, 3))
print("-"*35)
print('Sigma Value:\n',np.round(Sigma, 3))
print("-"*35)
print('V transpose matrix:\n',np.round(Vt, 3))
(4, 4) (4,) (4, 4)
-----------------------------------
U matrix:
[[ 0.246 0.583 -0.071 -0.771]
[-0.774 -0.017 0.551 -0.31 ]
[-0.529 0.566 -0.551 0.31 ]
[ 0.246 0.583 0.623 0.461]]
-----------------------------------
Sigma Value:
[2.663 0.807 0. 0. ]
-----------------------------------
V transpose matrix:
[[ 0.164 -0.575 -0.782 -0.173]
[-0.68 0.194 -0.132 -0.695]
[-0.703 -0.444 0.056 0.553]
[-0.129 0.659 -0.606 0.426]]
-
선형종속인 행렬을 다시 SVD분해하였을 때, $\Sigma$의 랭크가 2로 감소되었다.
-
이를 다시 원본 행렬로 복원하되 전체 데이터가 아닌 대각원소가 있는 경우만을 포함해보자.
# U_: Sigma의 앞 2행에 대응되는 앞 2열만 추출
U_ = U[:, :2]
# Sigma_: 대각원소가 존재하는 부분만 추출
Sigma_ = np.diag(Sigma[:2])
# Vt_: Sigma의 앞 2행에 대응되는 앞 2행만 추출
Vt_ = Vt[:2, :]
print(U_.shape, Sigma_.shape, Vt_.shape)
print("-"*35)
# a_ 행렬 되돌리기
a_ = np.dot(np.dot(U_,Sigma_), Vt_)
print(np.round(a_, 3))
(4, 2) (2, 2) (2, 4)
-----------------------------------
[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.542 0.899 1.041 -0.073]
[-0.212 -0.285 -0.574 -0.44 ]]
-
원본 행렬이 잘 복원되었다.
-
이는 Compact SVD 방식으로 복원되었다고 생각하면 될 듯 하다.
4.2 Truncated SVD
# matrix: 6 x 5
np.random.seed(121)
matrix = np.random.random((6, 5))
print(matrix)
[[0.11133083 0.21076757 0.23296249 0.15194456 0.83017814]
[0.40791941 0.5557906 0.74552394 0.24849976 0.9686594 ]
[0.95268418 0.48984885 0.01829731 0.85760612 0.40493829]
[0.62247394 0.29537149 0.92958852 0.4056155 0.56730065]
[0.24575605 0.22573721 0.03827786 0.58098021 0.82925331]
[0.77326256 0.94693849 0.73632338 0.67328275 0.74517176]]
scipy 패키지
from scipy.sparse.linalg import svds
# Truncated SVD
num_components = 4
U_tr, Sigma_tr, Vt_tr = svds(matrix, k=num_components)
print('Truncated SVD 분해 행렬 차원:',U_tr.shape, Sigma_tr.shape, Vt_tr.shape)
print('Truncated SVD Sigma값 행렬:', Sigma_tr)
Truncated SVD 분해 행렬 차원: (6, 4) (4,) (4, 5)
Truncated SVD Sigma값 행렬: [0.38255758 0.77828423 0.97971693 3.02855319]
scipy.sparse.linalg패키지의svds()를 이용해서 Truncated SVD를 수행 가능하다.
# matrix 되돌리기
matrix_tr = U_tr @ np.diag(Sigma_tr) @ Vt_tr
print('nTruncated SVD로 분해 후 복원 행렬:\n', matrix_tr)
nTruncated SVD로 분해 후 복원 행렬:
[[0.0705565 0.21415534 0.24963208 0.1957102 0.81723789]
[0.36768743 0.5591333 0.76197182 0.29168327 0.95589127]
[0.90633052 0.49370017 0.03724788 0.9073604 0.39022737]
[0.63790101 0.29408972 0.92328154 0.38905666 0.57219663]
[0.30718373 0.22063345 0.01316463 0.51504603 0.84874816]
[0.81143082 0.94376726 0.72071921 0.63231437 0.75728494]]
-
Truncated SVD 방법은 $\Sigma$의 대각원소가 0이 아니어도 제외한다.
-
따라서 행렬 복원시 완벽하게 복원되지 않고 근사적으로 복원된다.
4.3 PCA/TSVD
4.3.1 피처 스케일링 전 비교
from sklearn.decomposition import TruncatedSVD, PCA
from sklearn.datasets import load_iris
iris = load_iris()
iris_ftrs = iris.data
# TruncatedSVD 변환
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_ftrs)
iris_tsvd = tsvd.transform(iris_ftrs)
# PCA 변환
pca = PCA(n_components=2)
pca.fit(iris_ftrs)
iris_pca = pca.transform(iris_ftrs)
# 데이터 프레임 생성
iris_df = pd.DataFrame(np.concatenate([iris_tsvd, iris_pca], axis=1))
iris_df.columns = ["TSVD_C1", "TSVD_C2", "PCA_C1", "PCA_C2"]
iris_df["target"] = iris.target
iris_df.head()
| TSVD_C1 | TSVD_C2 | PCA_C1 | PCA_C2 | target | |
|---|---|---|---|---|---|
| 0 | 5.912747 | 2.302033 | -2.684126 | 0.319397 | 0 |
| 1 | 5.572482 | 1.971826 | -2.714142 | -0.177001 | 0 |
| 2 | 5.446977 | 2.095206 | -2.888991 | -0.144949 | 0 |
| 3 | 5.436459 | 1.870382 | -2.745343 | -0.318299 | 0 |
| 4 | 5.875645 | 2.328290 | -2.728717 | 0.326755 | 0 |
-
sklearn.decomposition패키지의TruncatedSVD()는 $U$, $\Sigma$, $V^{T}$를 반환하진 않는다. -
PCA()처럼fit(),transform()으로 원본 데이터를 주요 컴포넌트로 차원을 축소하여 변환해준다.
fig, axs = plt.subplots(1,2, figsize=(15,8))
# Truncated SVD 컴포넌트 시각화
sns.scatterplot(x="TSVD_C1", y="TSVD_C2", data=iris_df,
hue= "target", style = "target", ax = axs[0])
axs[0].set_title('Truncated SVD Transformed')
# PCA 컴포넌트 시각화
sns.scatterplot(x="PCA_C1", y="PCA_C2", data=iris_df,
hue= "target", style = "target", ax = axs[1])
axs[1].set_title('PCA Transformed')
plt.show()
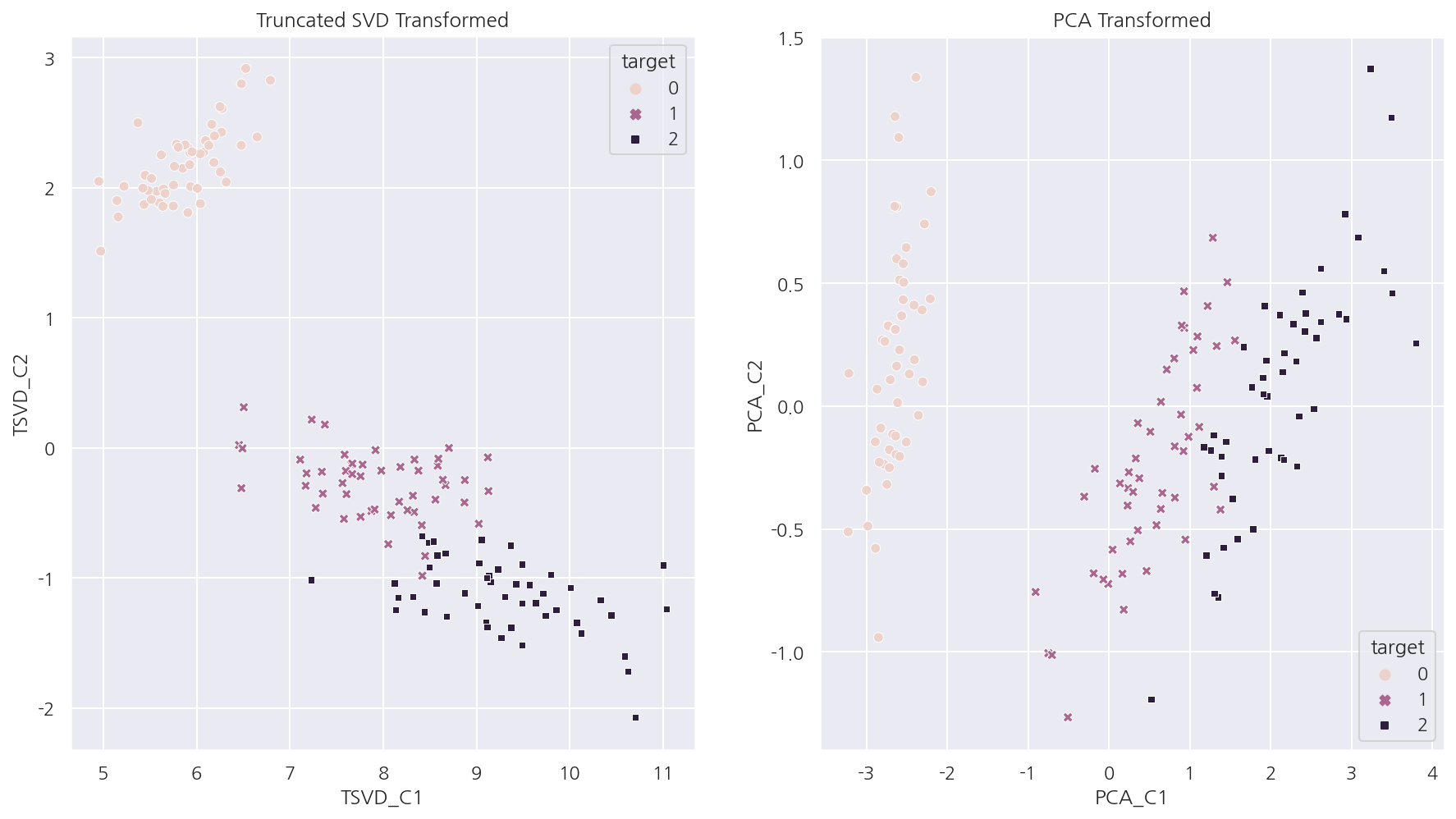
-
Truncated SVD 그래프를 보면 TSVD_C2 축을 기반으로 모든 붓꽃 품종이 어느정도 잘 분류된다.
-
Truncated SVD 역시 PCA처럼 어느 정도 분류가 가능하게끔 차원을 축소한다는 것을 알 수 있다.
4.3.2 피처 스케일링 후 비교
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# 피처 스케일링
scaler = StandardScaler()
iris_scaled = scaler.fit_transform(iris_ftrs)
# TruncatedSVD 변환
tsvd = TruncatedSVD(n_components=2)
tsvd.fit(iris_scaled)
iris_tsvd = tsvd.transform(iris_scaled)
# PCA 변환
pca = PCA(n_components=2)
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)
# 데이터 프레임 생성
iris_fin = pd.DataFrame(np.concatenate([iris_tsvd, iris_pca], axis=1))
iris_fin.columns = ["TSVD_C1", "TSVD_C2", "PCA_C1", "PCA_C2"]
iris_fin["target"] = iris.target
iris_fin.head()
| TSVD_C1 | TSVD_C2 | PCA_C1 | PCA_C2 | target | |
|---|---|---|---|---|---|
| 0 | -2.264703 | 0.480027 | -2.264703 | 0.480027 | 0 |
| 1 | -2.080961 | -0.674134 | -2.080961 | -0.674134 | 0 |
| 2 | -2.364229 | -0.341908 | -2.364229 | -0.341908 | 0 |
| 3 | -2.299384 | -0.597395 | -2.299384 | -0.597395 | 0 |
| 4 | -2.389842 | 0.646835 | -2.389842 | 0.646835 | 0 |
fig, axs = plt.subplots(1,2, figsize=(15,8))
# Truncated SVD 컴포넌트 시각화
sns.scatterplot(x="TSVD_C1", y="TSVD_C2", data=iris_fin,
hue= "target", style = "target", ax = axs[0])
axs[0].set_title('Truncated SVD Transformed')
# PCA 컴포넌트 시각화
sns.scatterplot(x="PCA_C1", y="PCA_C2", data=iris_fin,
hue= "target", style = "target", ax = axs[1])
axs[1].set_title('PCA Transformed')
plt.show()
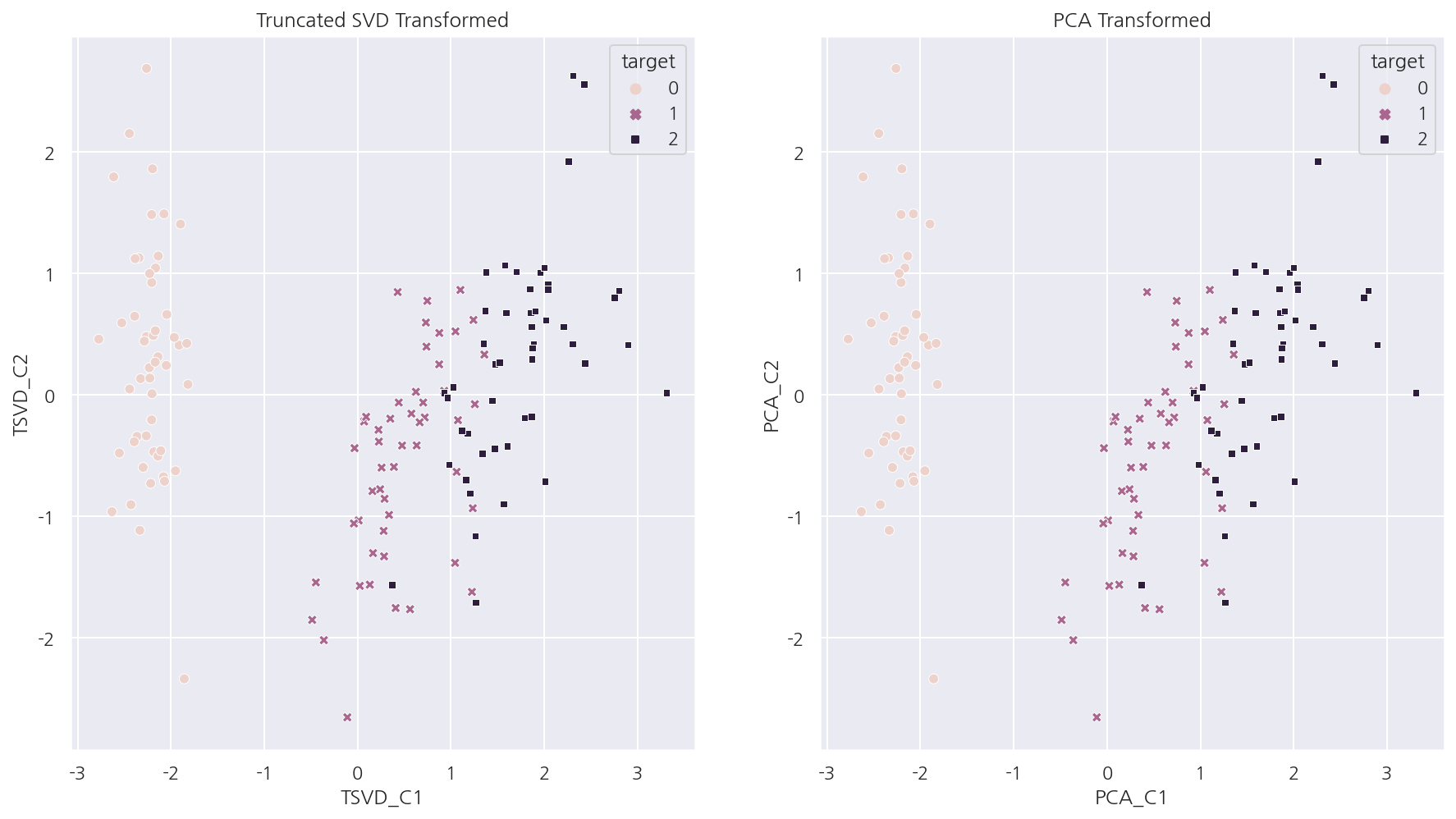
-
피처 스케일링 이후 Truncated SVD와 PCA로 컴포넌트를 구한 후 시각화 하였다.
-
두 방법의 결과가 거의 동일함을 알 수 있다.
# 두 방법의 컴포넌트 차이 평균
var1 = (iris_pca - iris_tsvd).mean()
print(f"{var1:.3f}")
# 원본 피처별 컴포넌트 비율 차이 평균
var2 = (pca.components_ - tsvd.components_).mean()
print(f"{var2:.3f}")
0.000
-0.000
-
직접 컴포넌트 값의 차이와 원본 피처별 컴포넌트 비율 값의 차이를 계산하였다.
-
모두 0에 가까운 값으로 두 방법의 결과가 동일함을 알 수 있다.
-
즉, 데이터 스케일링을 통해 데이터 중심이 동일해지면 두 방법은 동일한 변환값을 반환한다.

Leave a comment