[Python] 데이터 사이언스 스쿨 - 4.1 회귀분석 예제
Updated:
데이터 사이언스 스쿨 자료를 토대로 공부한 내용입니다.
실습과정에서 필요에 따라 내용의 누락 및 추가, 수정사항이 있습니다.
기본 세팅
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
mpl.rc('font', family='NanumGothic') # 폰트 설정
mpl.rc('axes', unicode_minus=False) # 유니코드에서 음수 부호 설정
# 차트 스타일 설정
sns.set(font="NanumGothic", rc={"axes.unicode_minus":False}, style='darkgrid')
plt.rc("figure", figsize=(10,8))
warnings.filterwarnings("ignore")
4.1 회귀분석 예제
4.1.1 보스턴 집값 예측
sklearn 패키지의 datasets 서브패키지는 회귀분석을 공부하기 위한 예제를 제공한다.
그 중 load_boston() 명령으로 받을 수 있는 보스턴 주택 가격 데이터는 다음과 같은 데이터이다.
보스턴의 506개 타운(town)의 13개 독립변수값로부터 해당 타운의 주택가격 중앙값을 예측하는 문제다.
사용할 수 있는 특징 데이터는 다음과 같다.
| 변수 | 설명 |
|---|---|
| CRIM | 범죄율 |
| INDUS | 비소매상업지역 면적 비율 |
| NOX | 일산화질소 농도 |
| RM | 주택당 방 수 |
| LSTAT | 인구 중 하위 계층 비율 |
| B | 인구 중 흑인 비율 |
| PTRATIO | 학생/교사 비율 |
| ZN | 25,000 평방피트를 초과 거주지역 비율 |
| CHAS | 찰스강의 경계에 위치한 경우는 1, 아니면 0 |
| AGE | 1940년 이전에 건축된 주택의 비율 |
| RAD | 방사형 고속도로까지의 거리 |
| DIS | 직업센터의 거리 |
| TAX | 재산세율 |
| MEDV | 보스턴 506개 타운의 1978년 주택 가격 중앙값 (단위 1,000 달러) |
종속변수는 MEDV로 사실 원래 변수명이 따로 없이 저장되어 있는데 밑에 실습에서 MEDV로 지정할 것이다.
Boston 데이터 불러오기
from sklearn.datasets import load_boston
temp = load_boston()
dir(temp)
['DESCR', 'data', 'feature_names', 'filename', 'target']
load_boston() 명령으로 받는 데이터 집합은 Bunch 라는 클래스 객체로 생성된다.
이 클래스 객체는 다음과 같은 속성을 가진다.
-
data: 독립변수 ndarray 배열 -
target: 종속변수 ndarray 배열 -
feature_names: 독립변수 이름 리스트 -
target_names: (옵션) 종속변수 이름 리스트 -
DESCR: (옵션) 자료에 대한 설명 문자열
x_data = pd.DataFrame(temp.data, columns = temp.feature_names)
y_data = pd.DataFrame(temp.target, columns = ["MEDV"])
boston = pd.concat([x_data, y_data], axis = 1)
boston.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | MEDV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 | 36.2 |
-
load_boston()의 여러 속성을 이용해서 boston 데이터 프레임을 생성하였다. -
종속 변수는 MEDV로 이름을 지정하였다.
일부 변수 시각화
sns.pairplot(boston[["MEDV", "RM", "AGE"]])
plt.suptitle("Boston Pair Plot, 일부 독립변수와 종속변수 시각화", y=1.03)
plt.show()
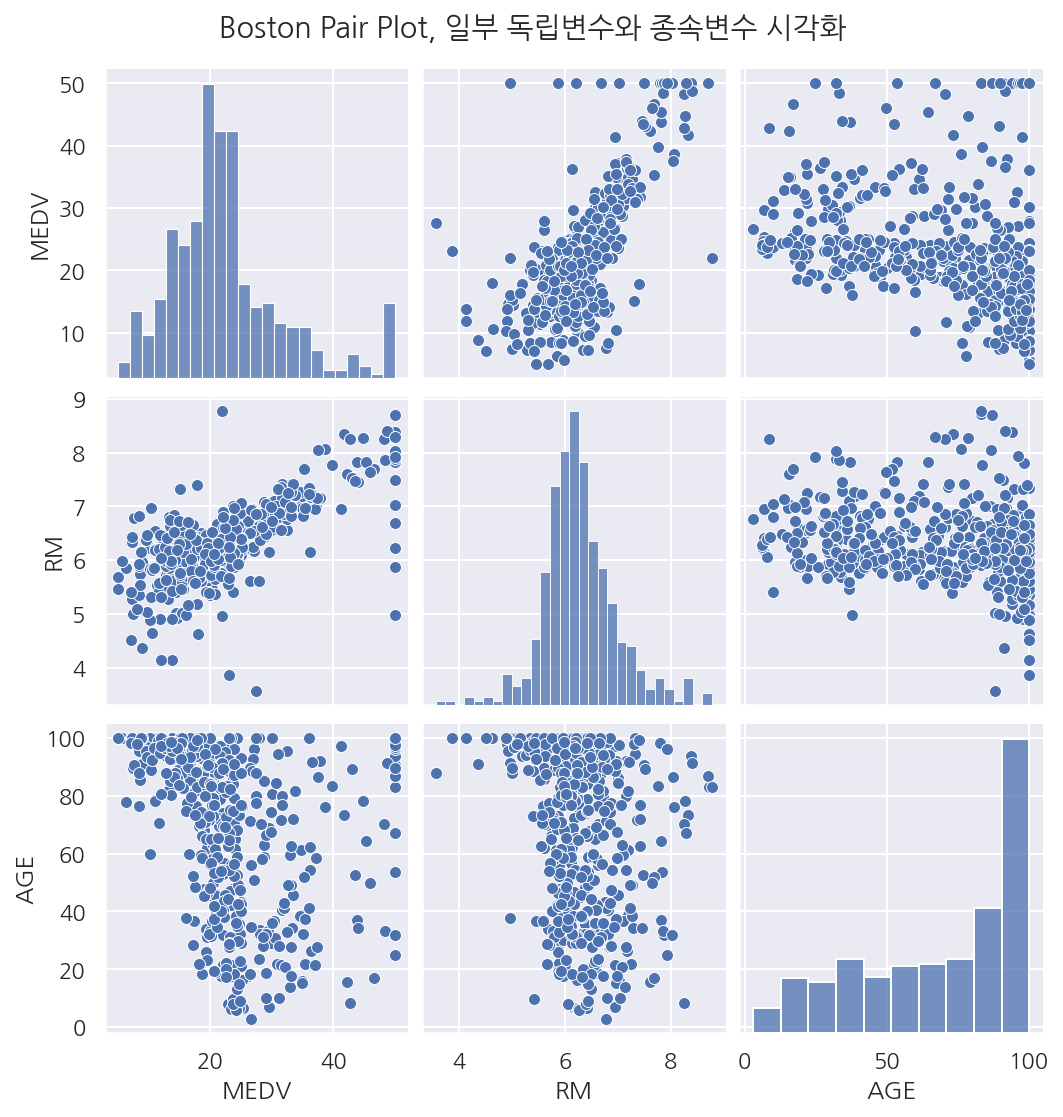
-
방 개수(RM)가 증가할 수록 집값(MEDV)은 증가하는 경향이 보인다.
-
노후화 정도(AGE)와 집값은 관계(MEDV)가 없어 보인다.
4.1.2 당뇨병 진행도 예측
scikit-learn 패키지가 제공하는 당뇨병 진행도 예측용 데이터는 442명의 당뇨병 환자를 대상으로한 검사 결과를 나타내는 데이터이다.
| 변수 | 설명 |
|---|---|
| age | 나이 |
| sex | 성별 |
| bmi | BMI(Body mass index)지수 |
| bp | 평균혈압 |
| s1~s6 | 6종류의 혈액검사수치 |
| 종속변수 | 1년 뒤 측정한 당뇨병의 진행률 |
Diabetes 데이터 불러오기
from sklearn.datasets import load_diabetes
temp = load_diabetes()
diabetes = pd.DataFrame(temp.data, columns=temp.feature_names)
diabetes["target"] = temp.target
diabetes.tail()
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | target | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 437 | 0.041708 | 0.050680 | 0.019662 | 0.059744 | -0.005697 | -0.002566 | -0.028674 | -0.002592 | 0.031193 | 0.007207 | 178.0 |
| 438 | -0.005515 | 0.050680 | -0.015906 | -0.067642 | 0.049341 | 0.079165 | -0.028674 | 0.034309 | -0.018118 | 0.044485 | 104.0 |
| 439 | 0.041708 | 0.050680 | -0.015906 | 0.017282 | -0.037344 | -0.013840 | -0.024993 | -0.011080 | -0.046879 | 0.015491 | 132.0 |
| 440 | -0.045472 | -0.044642 | 0.039062 | 0.001215 | 0.016318 | 0.015283 | -0.028674 | 0.026560 | 0.044528 | -0.025930 | 220.0 |
| 441 | -0.045472 | -0.044642 | -0.073030 | -0.081414 | 0.083740 | 0.027809 | 0.173816 | -0.039493 | -0.004220 | 0.003064 | 57.0 |
일부 변수 시각화
sns.pairplot(diabetes[["target", "bmi", "bp", "s1"]])
plt.suptitle("Diabetes Pair Plot, 일부 독립변수와 종속변수 시각화", y=1.03)
plt.show()
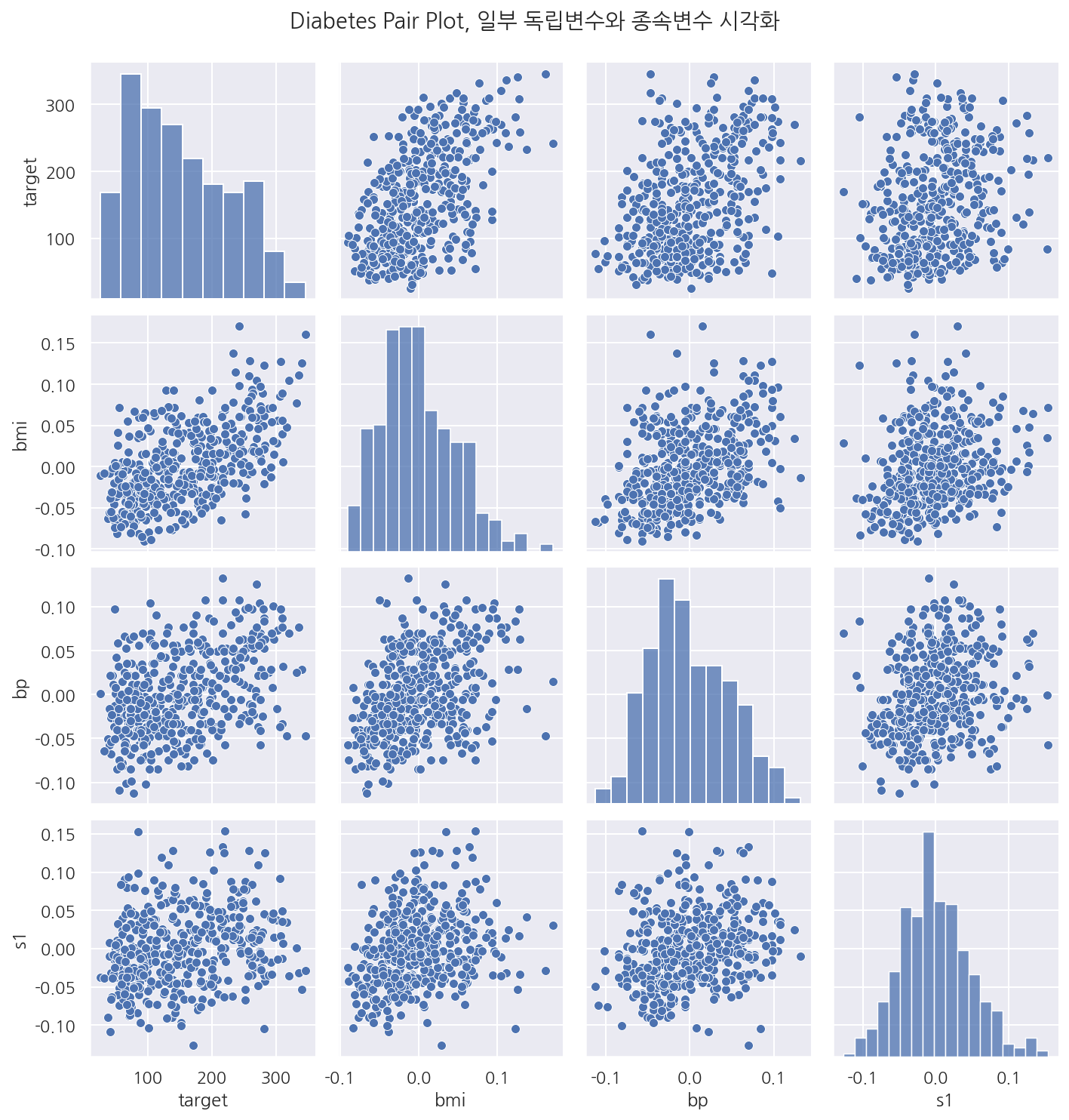
-
독립변수 BMI지수와 평균혈압은 종속변수인 당뇨병 진행도와 양의 상관관계를 가지는 것을 볼 수 있다.
-
독립변수 BMI지수와 평균혈압도 서로 양의 상관관계를 가져 다중공선성이 보인다.
4.1.3 연습문제
sklearn.datasets 패키지의 fetch_california_housing 명령은 캘리포니아 주택가격을 예측하기위한 데이터다.
이 데이터의 독립변수를 조사하고 어떤 데이터들이 주택가격과 상관관계가 있는지를 조사한다.
또한 서로 강한 상관관계를 가지는 독립변수도 알아보자.
California 데이터 불러오기
from sklearn.datasets import fetch_california_housing
temp = fetch_california_housing()
california = pd.DataFrame(temp.data, columns=temp.feature_names)
california["MedHouseVal"] = temp.target
california.tail()
| MedInc | HouseAge | AveRooms | AveBedrms | Population | AveOccup | Latitude | Longitude | MedHouseVal | |
|---|---|---|---|---|---|---|---|---|---|
| 20635 | 1.5603 | 25.0 | 5.045455 | 1.133333 | 845.0 | 2.560606 | 39.48 | -121.09 | 0.781 |
| 20636 | 2.5568 | 18.0 | 6.114035 | 1.315789 | 356.0 | 3.122807 | 39.49 | -121.21 | 0.771 |
| 20637 | 1.7000 | 17.0 | 5.205543 | 1.120092 | 1007.0 | 2.325635 | 39.43 | -121.22 | 0.923 |
| 20638 | 1.8672 | 18.0 | 5.329513 | 1.171920 | 741.0 | 2.123209 | 39.43 | -121.32 | 0.847 |
| 20639 | 2.3886 | 16.0 | 5.254717 | 1.162264 | 1387.0 | 2.616981 | 39.37 | -121.24 | 0.894 |
상관관계 확인
corr_M = california.corr()
mask = np.array(corr_M)
mask[np.tril_indices_from(mask)] = False
plt.figure(figsize= (10,8))
sns.heatmap(corr_M,
cmap = sns.light_palette("red", as_cmap=True),
annot = True,
mask = mask)
plt.show()
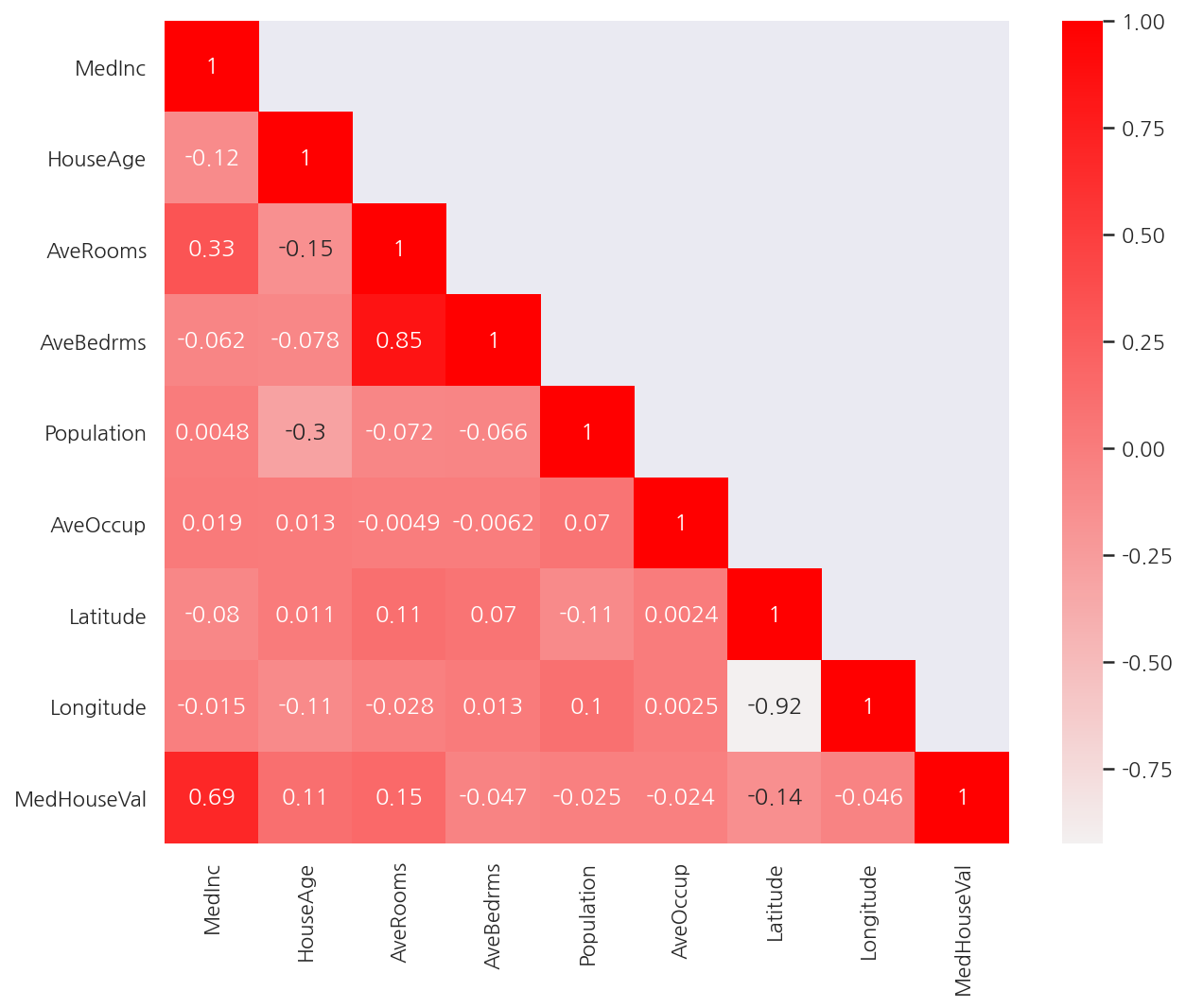
-
종속변수 MedHouseVal와 상관관계가 높은 독립변수는 MedInc이다.
-
독립변수간에는 AveRooms와 AveBedrms, Latitude와 Longitude가 서로 강한 상관관계를 가지고 있다.
일부 변수 시각화
sns.pairplot(california[["MedHouseVal", "MedInc", "AveRooms", "AveBedrms", "Latitude", "Longitude"]])
plt.suptitle("California Pair Plot, 일부 독립변수와 종속변수 시각화", y=1.03)
plt.show()
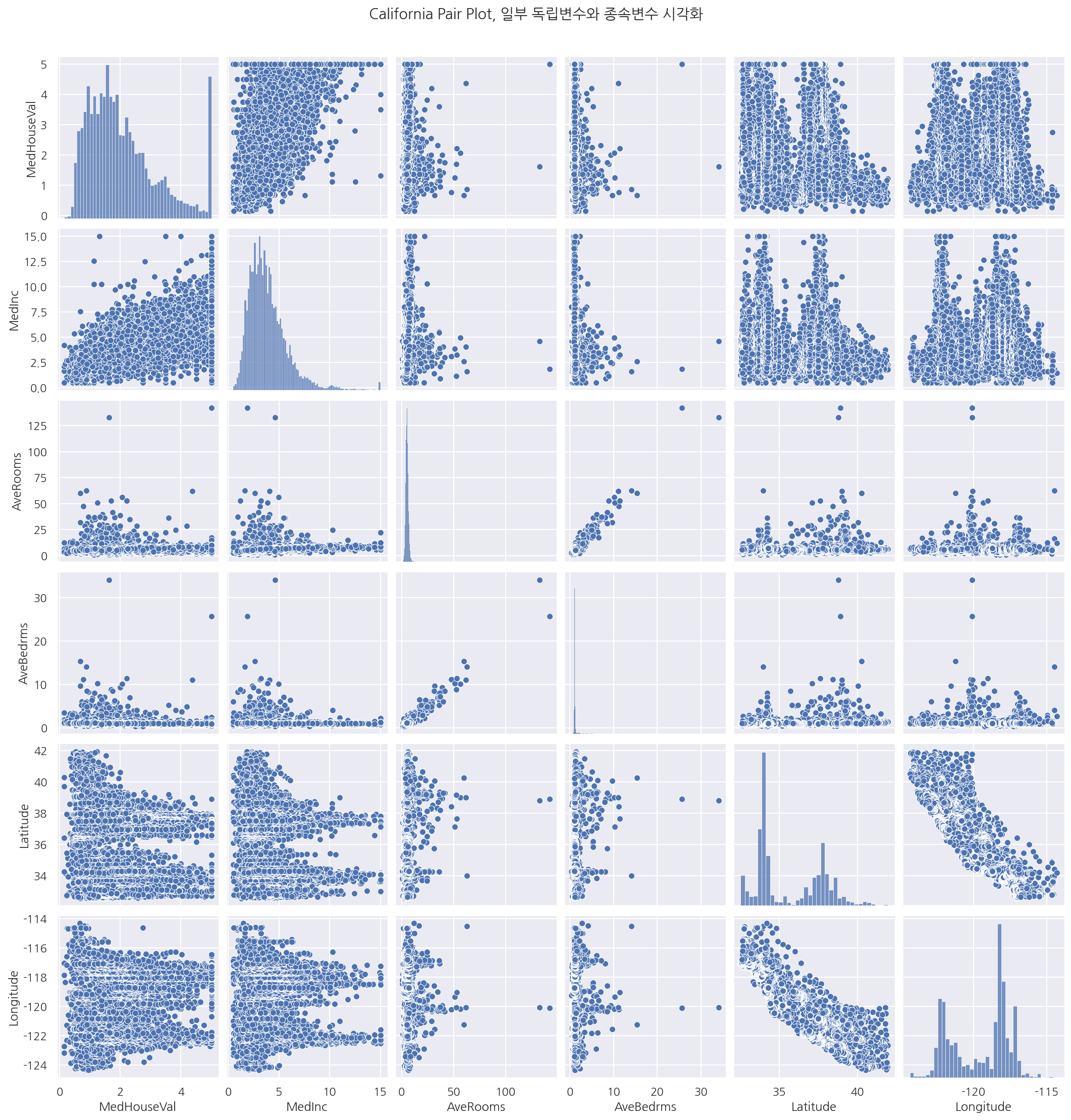
-
상관계수로 확인 하였듯이 변수간 선형관계가 보인다.
-
Latitude와 Longitude는 비선형 형태에 가까워 보인다.
4.1.4 가상 데이터 예측
가상 데이터 만들기
datasets 서브패키지에는 가상 회귀 분석 예제를 만들 수 있는 make_regression() 함수가 있다.
해당 함수에 대한 설명은 다음과 같다.
X, Y, B = make_regression(
n_samples, n_features, bias, noise, random_state, coef=True, n_informative, effective_rank, tail_strength)
| 옵션 | 입력 자료형 | 설명 |
|---|---|---|
| n_samples | 정수(디폴트 100) | 표본 데이터의 갯수 n |
| n_features | 정수(디폴트 100) | 독립변수의 수 p |
| bias | 실수(디폴트 0) | Y 절편 |
| noise | 실수(디폴트 0) | 오차항의 표준편차 $\epsilon$의 표준편차 |
| random_state | 정수(디폴트 None) | 난수 발생용 시드값 |
| coef | 불리언(디폴트 False) | True면 회귀 계수 출력 |
| n_informative | 정수(디폴트 10) | 독립변수 중 종속변수와 상관 관계가 있는 독립변수의 수 |
| effective_rank | 정수 또는 None(디폴트 None) | 독립변수 중 서로 독립인 독립변수의 수. 만약 None이면 모두 독립 |
| tail_strength | 0~1사이의 실수(디폴트 0.5) | effective_rank가 None이 아닌 경우 독립변수간의 상관관계를 결정하는 변수. 0.5면 독립변수간의 상관관계가 없다. |
출력은 다음과 같다.
-
X: (n_samples, n_features) 형상의 2차원 배열로 독립변수의 표본 데이터 행렬 $X$, n x p
-
Y: (n_samples) 형상의 1차원 배열로 종속변수의 표본 데이터 벡터 $Y$, n x 1
-
B: (n_features) 형상의 1차원 배열로 선형 모형의 계수 벡터 $\beta$, p x 1
혹은 (n_features, n_targets) 형상의 2차원 배열 (옵션) 입력 인수 coef가 True 인 경우에만 출력됨 - 절편 제외
from sklearn.datasets import make_regression
X, Y, B = make_regression(
n_samples=200, n_features=1, bias=2, noise=10, coef=True, random_state=1017
)
x = np.linspace(-3, 3, 100)
y0 = B * x + 2
plt.figure(figsize= (10,8))
# 회귀식 - 오차항 고려없이 계수로 생성, 모수 beta를 이미 알고 있음
plt.plot(x, y0, "r-")
# 산점도
plt.scatter(X, Y)
plt.xlabel("x")
plt.ylabel("y")
plt.title("make_regression 예제")
plt.show()
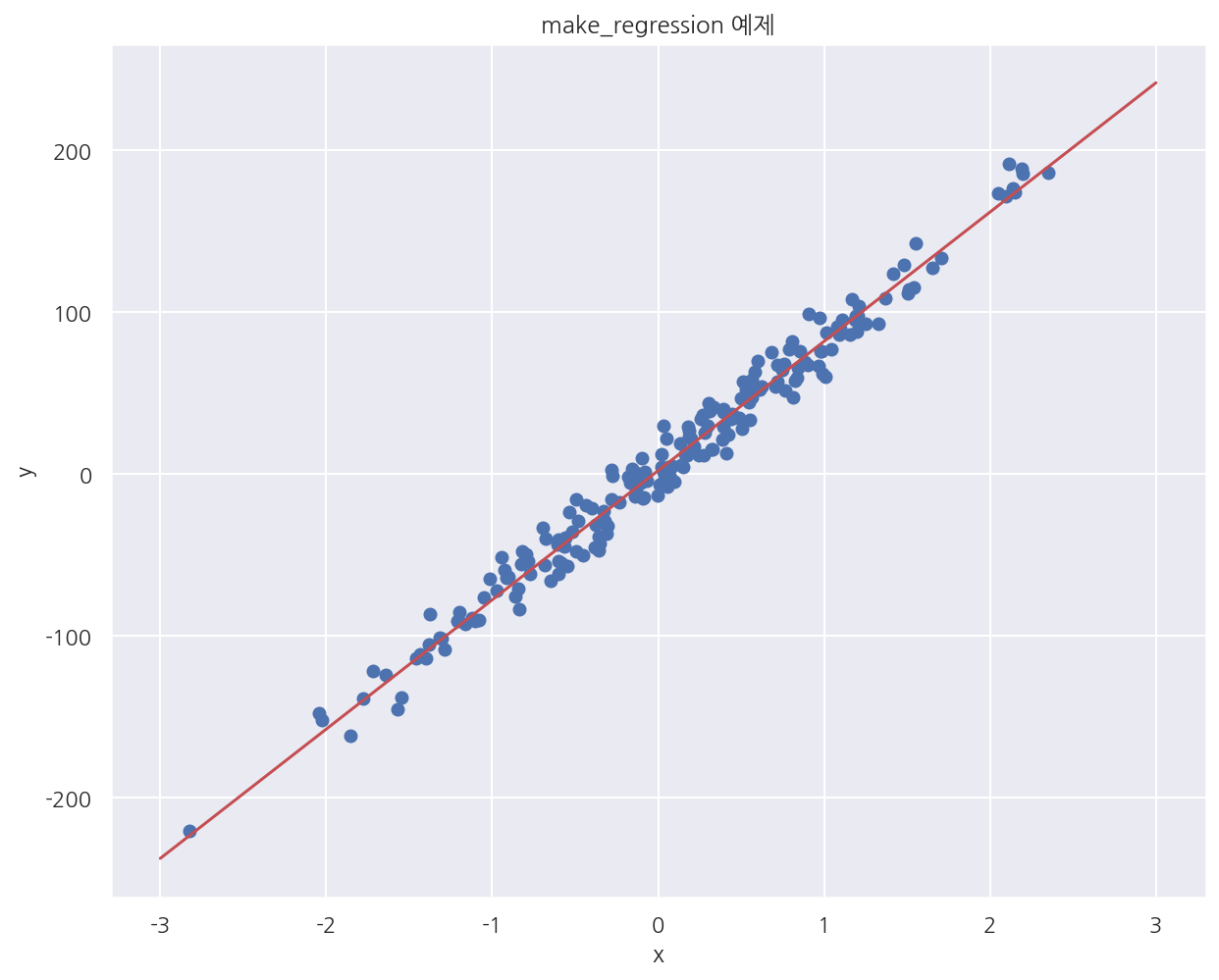
-
make_regression()으로 만든 가상 데이터 산점도이다. -
독립변수는 1개, 절편은 2, 오차항의 표준편차는 10으로 설정하였다.
-
오차항 고려 없이 만든 직선을 기준으로 데이터가 잘 퍼져있다.
def make_regression2(n_informative, effective_rank, tail_strength, i):
X, Y, B = make_regression(
n_samples=300, n_features=2, noise=10, coef=True, random_state=0,
n_informative = n_informative, effective_rank= effective_rank, tail_strength = tail_strength
)
axs[i].scatter(X[:, 0], X[:, 1], c=Y, s=100, cmap=mpl.cm.bone)
axs[i].set_xlabel("x1")
axs[i].set_ylabel("x2")
fig, axs = plt.subplots(1,3, figsize= (15,6))
make_regression2(2,None,0.5, 0)
make_regression2(1,None,0.5, 1)
make_regression2(2,1,0, 2)
plt.axis("equal")
axs[0].set_title("독립변수: 서로 독립, 종속변수와 모두 상관 관계")
axs[1].set_title("독립변수: 서로 독립, 종속변수와 하나만 상관 관계")
axs[2].set_title("독립변수가 독립이 아닌 경우")
plt.show()
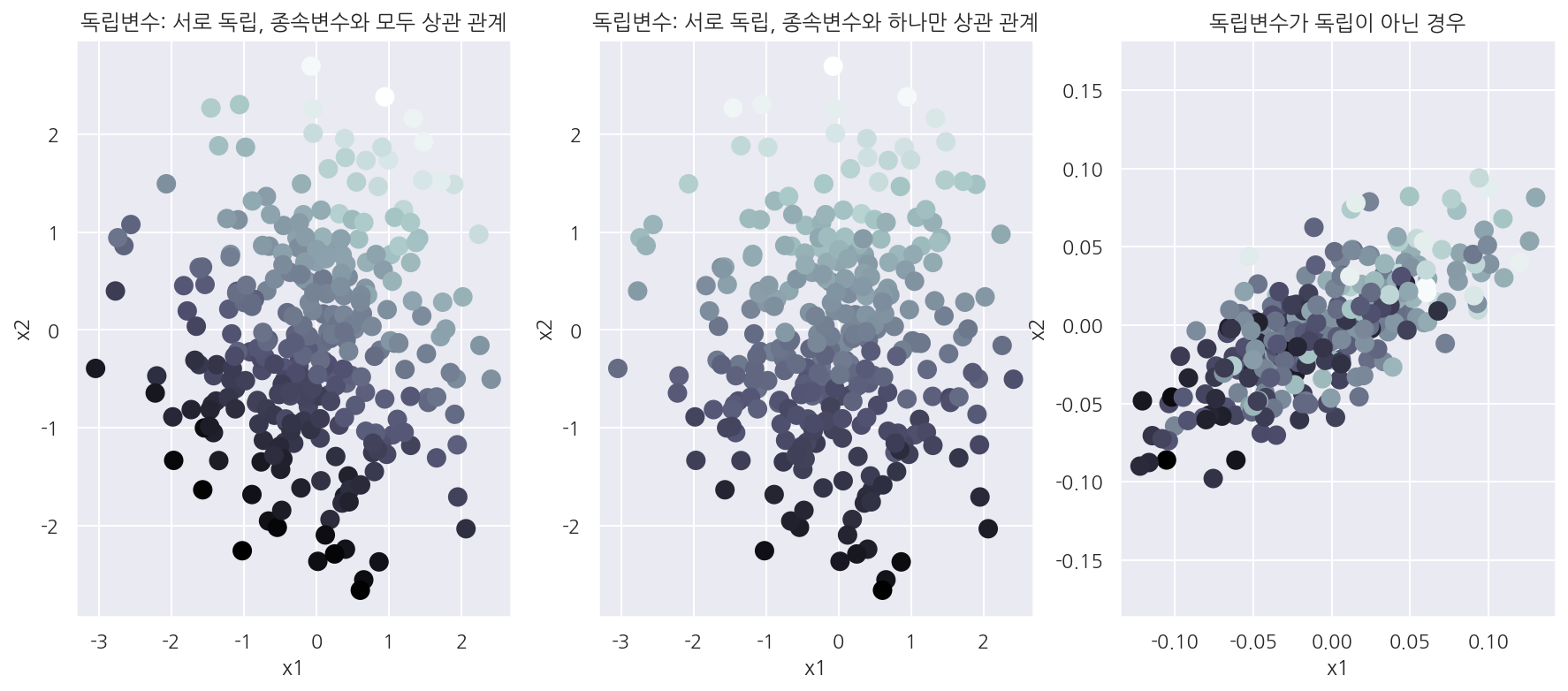
-
종속변수 값은 점의 명암으로 표시하였으며 밝을수록 종속변수 값이 큰 것이고 점의 어두울수록 작은 값이다.
-
첫 번째 산점도에선 x1, x2 모두 증가할수록 종속변수 값이 커지는 것을 알 수 있다.
-
두 번째 산점도에선 x2가 증가할수록 종속변수 값이 증가하지만 x1에 따라선 큰 차이가 없다.
-
세 번쨰 산점도에선 x1, x2가 상관관계를 가지는 것을 확인 할 수 있다.

Leave a comment