[Python] 데이터 사이언스 스쿨 - 데이터 전처리
Updated:
데이터 사이언스 스쿨 자료를 토대로 공부한 내용입니다.
실습과정에서 필요에 따라 내용의 누락 및 추가, 수정사항이 있습니다.
기본 세팅
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
mpl.rc('font', family='NanumGothic') # 폰트 설정
mpl.rc('axes', unicode_minus=False) # 유니코드에서 음수 부호 설정
# 차트 스타일 설정
sns.set(font="NanumGothic", rc={"axes.unicode_minus":False}, style='darkgrid')
plt.rc("figure", figsize=(10,8))
warnings.filterwarnings("ignore")
1. 데이터 전처리 기초
1.1 결측값 확인
from io import StringIO
csv_data = StringIO("""
x1,x2,x3,x4,x5
1,0.1,"1",2019-01-01,A
2,,,2019-01-02,B
3,,"3",2019-01-03,C
,0.4,"4",2019-01-04,A
5,0.5,"5",2019-01-05,B
,,,2019-01-06,C
7,0.7,"7",,A
8,0.8,"8",2019-01-08,B
9,0.9,,2019-01-09,C
""")
df = pd.read_csv(csv_data, dtype={"x1": pd.Int64Dtype()}, parse_dates=[3])
df
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 0 | 1 | 0.1 | 1.0 | 2019-01-01 | A |
| 1 | 2 | NaN | NaN | 2019-01-02 | B |
| 2 | 3 | NaN | 3.0 | 2019-01-03 | C |
| 3 | <NA> | 0.4 | 4.0 | 2019-01-04 | A |
| 4 | 5 | 0.5 | 5.0 | 2019-01-05 | B |
| 5 | <NA> | NaN | NaN | 2019-01-06 | C |
| 6 | 7 | 0.7 | 7.0 | NaT | A |
| 7 | 8 | 0.8 | 8.0 | 2019-01-08 | B |
| 8 | 9 | 0.9 | NaN | 2019-01-09 | C |
-
결측값이 있는 임시 데이터를 생성하였다.
-
실제 데이터를 불러올때도 정수형, 날짜형 등 자료형태를 명시하는 것이 중요하다.
-
날짜형은 자료형태를 지정하지 않으면 object로 불러와 dt 인자를 적용할 수 없다.
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 9 entries, 0 to 8
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 x1 7 non-null Int64
1 x2 6 non-null float64
2 x3 6 non-null float64
3 x4 8 non-null datetime64[ns]
4 x5 9 non-null object
dtypes: Int64(1), datetime64[ns](1), float64(2), object(1)
memory usage: 497.0+ bytes
info()를 이용해서 데이터 프레임의 행, 열의 갯수, 결측값의 수, 자료형태 등을 확인 가능하다.
# 참고용
df.select_dtypes(exclude=['datetime'])
| x1 | x2 | x3 | x5 | |
|---|---|---|---|---|
| 0 | 1 | 0.1 | 1.0 | A |
| 1 | 2 | NaN | NaN | B |
| 2 | 3 | NaN | 3.0 | C |
| 3 | <NA> | 0.4 | 4.0 | A |
| 4 | 5 | 0.5 | 5.0 | B |
| 5 | <NA> | NaN | NaN | C |
| 6 | 7 | 0.7 | 7.0 | A |
| 7 | 8 | 0.8 | 8.0 | B |
| 8 | 9 | 0.9 | NaN | C |
-
위 코드는 참고용으로 적어두었다.
-
select_dtypes()에 exclude 옵션에 특정 자료형을 넣으면 해당 자료형을 제외한 열을 추출한다. -
반대로 exclude옵션 대신 include 옵션을 사용하면 지정한 자료형의 열만 추출한다.
df.isnull().sum()
x1 2
x2 3
x3 3
x4 1
x5 0
dtype: int64
isnull().sum()을 이용해 각 열마다 결측값의 개수를 확인 가능하다.
import missingno as msno
msno.matrix(df)
plt.show()

-
missingno데이터 프레임에서 결측 데이터를 찾는 기능을 제공한다. -
단, 이 패키지를 사용하려면 데이터프레임에 결측 데이터가 NaN으로 저장되어 있어야한다.
-
msno.matrix()를 이용해 결측 데이터 시각화가 가능하다. -
결측 데이터는 흰색, 결측이 아니면 검은색으로 나타난다.
msno.bar(df)
plt.show()
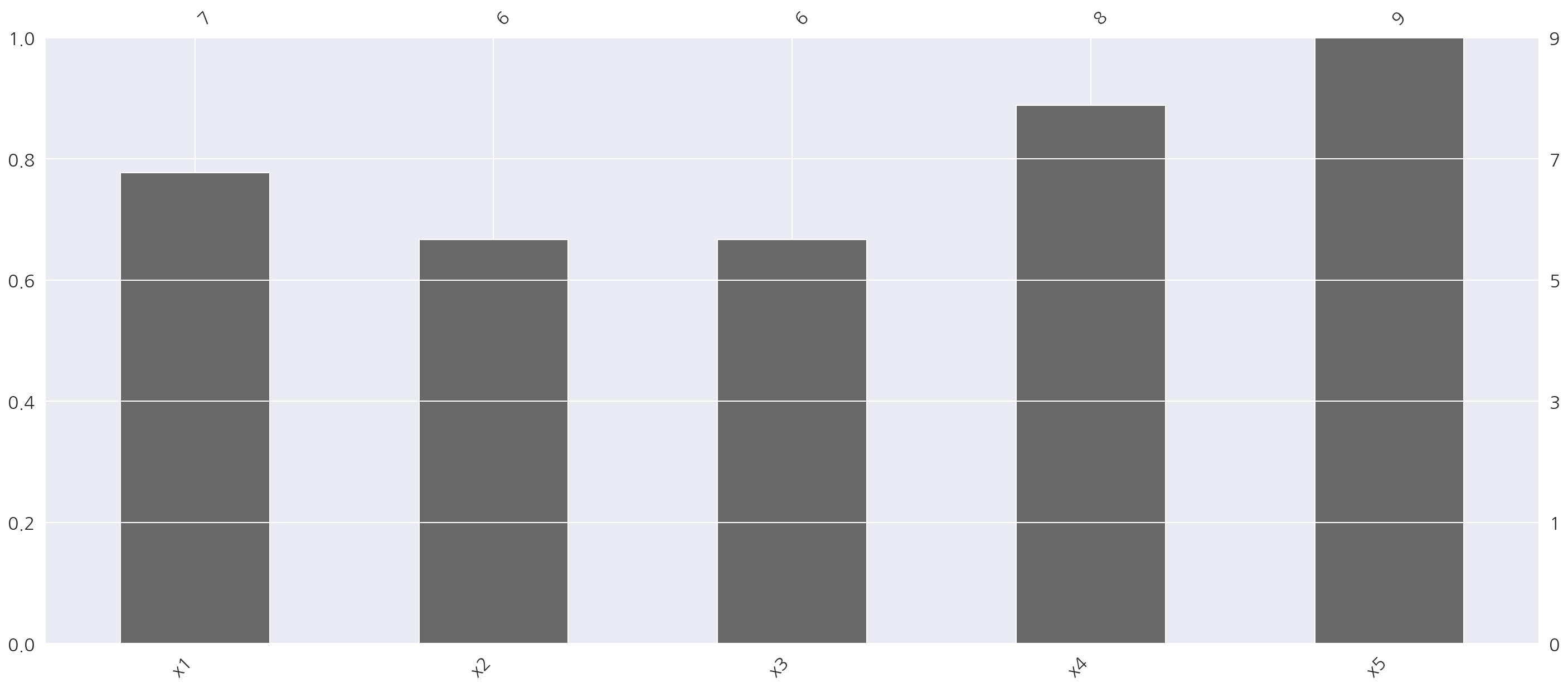
msno.bar()를 이용해 결측이 아닌 데이터의 갯수 시각화가 가능하다.
1.2 결측값 처리
1.2.1 결측값 삭제
df.dropna()
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 0 | 1 | 0.1 | 1.0 | 2019-01-01 | A |
| 4 | 5 | 0.5 | 5.0 | 2019-01-05 | B |
| 7 | 8 | 0.8 | 8.0 | 2019-01-08 | B |
dropna()를 이용해 결측값이 있는 행을 제거 가능하다.
df.dropna(axis=1)
| x5 | |
|---|---|
| 0 | A |
| 1 | B |
| 2 | C |
| 3 | A |
| 4 | B |
| 5 | C |
| 6 | A |
| 7 | B |
| 8 | C |
- axis=1 옵션을 이용해 결측값이 있는 열을 제거 가능하다.
df.dropna(thresh=7, axis=1)
| x1 | x4 | x5 | |
|---|---|---|---|
| 0 | 1 | 2019-01-01 | A |
| 1 | 2 | 2019-01-02 | B |
| 2 | 3 | 2019-01-03 | C |
| 3 | <NA> | 2019-01-04 | A |
| 4 | 5 | 2019-01-05 | B |
| 5 | <NA> | 2019-01-06 | C |
| 6 | 7 | NaT | A |
| 7 | 8 | 2019-01-08 | B |
| 8 | 9 | 2019-01-09 | C |
- thresh=n 과 axis 옵션을 이용해 n개 이상 비결측 데이터가 있는 행 또는 열만 남길수 있다.
1.2.2 결측값 대체
# 평균값, 중앙값, 최빈값, 상수값으로 대체
df.fillna({"x1": df.x1.mean(),
"x2": df.x2.median(),
"x3": df.x3.value_counts().sort_values(ascending=False).index[0],
"x4": pd.to_datetime("2019/01/07", format='%Y-%m-%d')}
)
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 0 | 1 | 0.1 | 1.0 | 2019-01-01 | A |
| 1 | 2 | 0.6 | 1.0 | 2019-01-02 | B |
| 2 | 3 | 0.6 | 3.0 | 2019-01-03 | C |
| 3 | 5 | 0.4 | 4.0 | 2019-01-04 | A |
| 4 | 5 | 0.5 | 5.0 | 2019-01-05 | B |
| 5 | 5 | 0.6 | 1.0 | 2019-01-06 | C |
| 6 | 7 | 0.7 | 7.0 | 2019-01-07 | A |
| 7 | 8 | 0.8 | 8.0 | 2019-01-08 | B |
| 8 | 9 | 0.9 | 1.0 | 2019-01-09 | C |
-
fillna()를 이용해서 각 변수별로 대체값을 지정 가능하다. -
여기선 x1, x2, x3, x4를 각각 평균값, 중앙값, 최빈값, 상수값으로 대체하였다.
from sklearn.impute import SimpleImputer
# 최빈값으로 수정
imp = SimpleImputer(missing_values = np.nan, strategy = "most_frequent")
col = ["x1","x2","x3"]
df[col] = imp.fit_transform(df[col])
df
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 0 | 1.0 | 0.1 | 1.0 | 2019-01-01 | A |
| 1 | 2.0 | 0.1 | 1.0 | 2019-01-02 | B |
| 2 | 3.0 | 0.1 | 3.0 | 2019-01-03 | C |
| 3 | 1.0 | 0.4 | 4.0 | 2019-01-04 | A |
| 4 | 5.0 | 0.5 | 5.0 | 2019-01-05 | B |
| 5 | 1.0 | 0.1 | 1.0 | 2019-01-06 | C |
| 6 | 7.0 | 0.7 | 7.0 | NaT | A |
| 7 | 8.0 | 0.8 | 8.0 | 2019-01-08 | B |
| 8 | 9.0 | 0.9 | 1.0 | 2019-01-09 | C |
-
sklearn패키지의SimpleImputer()를 사용하여 결측값에 대체가 가능하다. -
strategy 옵션으로 평균, 중앙값, 최빈값, 상수값 등을 사용가능하다.
SimpleImputer(strategy = 'mean') # 평균
SimpleImputer(strategy = 'median') # 중앙값
SimpleImputer(strategy = 'most_frequent') # 최빈값
SimpleImputer(strategy = 'constant', fill_value=1) # 상수값
- 다만 날짜형에 대해서는 대체가 안되고 계속 에러가 발생했는데 검색을 해도 못찾겠어서 우선 비워두었다..
1.3 타이타닉 예제
# titanic 데이터 불러오기
titanic = sns.load_dataset("titanic")
titanic.tail()
| survived | pclass | sex | age | sibsp | parch | fare | embarked | class | who | adult_male | deck | embark_town | alive | alone | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 886 | 0 | 2 | male | 27.0 | 0 | 0 | 13.00 | S | Second | man | True | NaN | Southampton | no | True |
| 887 | 1 | 1 | female | 19.0 | 0 | 0 | 30.00 | S | First | woman | False | B | Southampton | yes | True |
| 888 | 0 | 3 | female | NaN | 1 | 2 | 23.45 | S | Third | woman | False | NaN | Southampton | no | False |
| 889 | 1 | 1 | male | 26.0 | 0 | 0 | 30.00 | C | First | man | True | C | Cherbourg | yes | True |
| 890 | 0 | 3 | male | 32.0 | 0 | 0 | 7.75 | Q | Third | man | True | NaN | Queenstown | no | True |
결측값 확인
titanic.isnull().sum()
survived 0
pclass 0
sex 0
age 177
sibsp 0
parch 0
fare 0
embarked 2
class 0
who 0
adult_male 0
deck 688
embark_town 2
alive 0
alone 0
dtype: int64
msno.matrix(titanic)
plt.title("Titanic Missing Data", fontsize = 20)
plt.show()
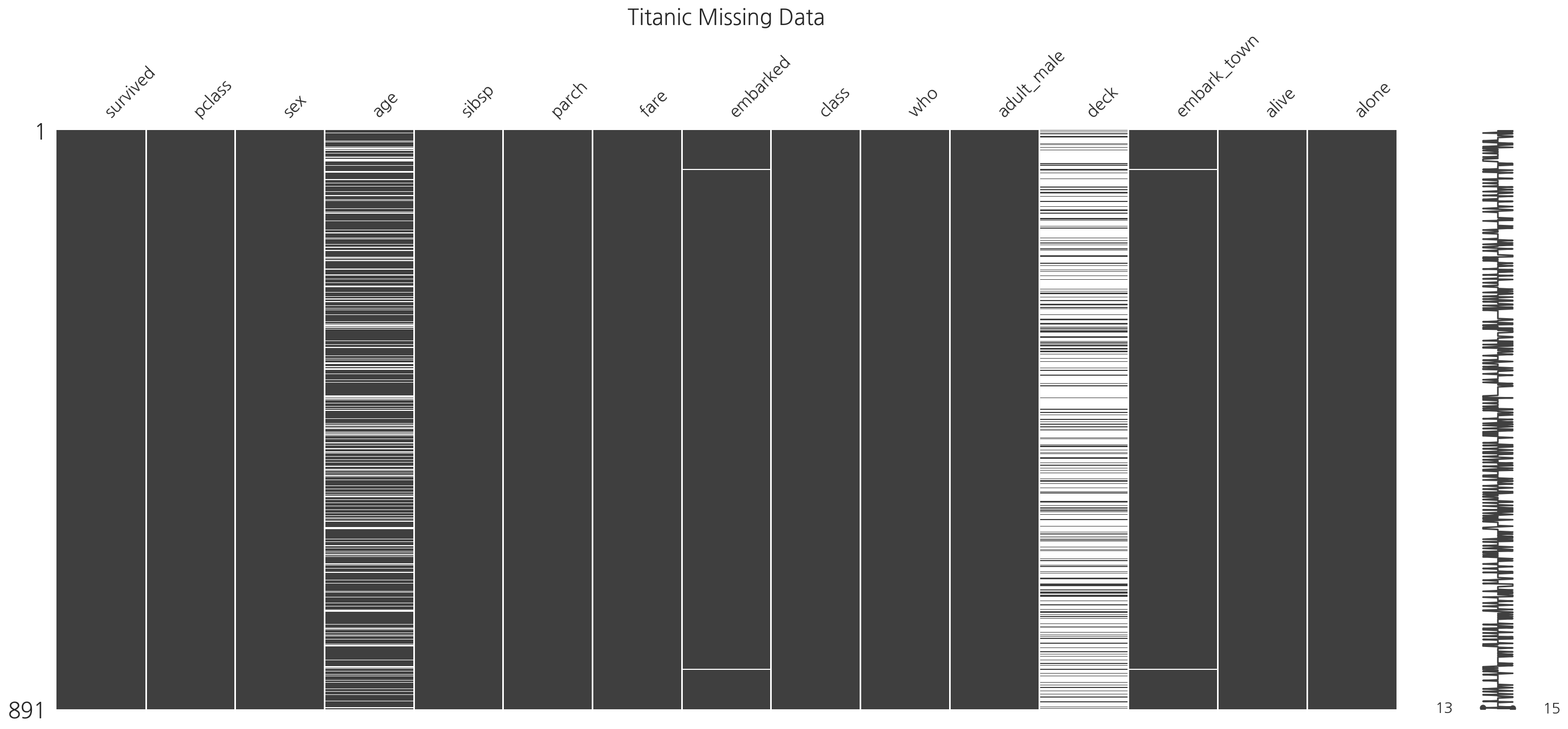
msno.bar(titanic)
plt.show()
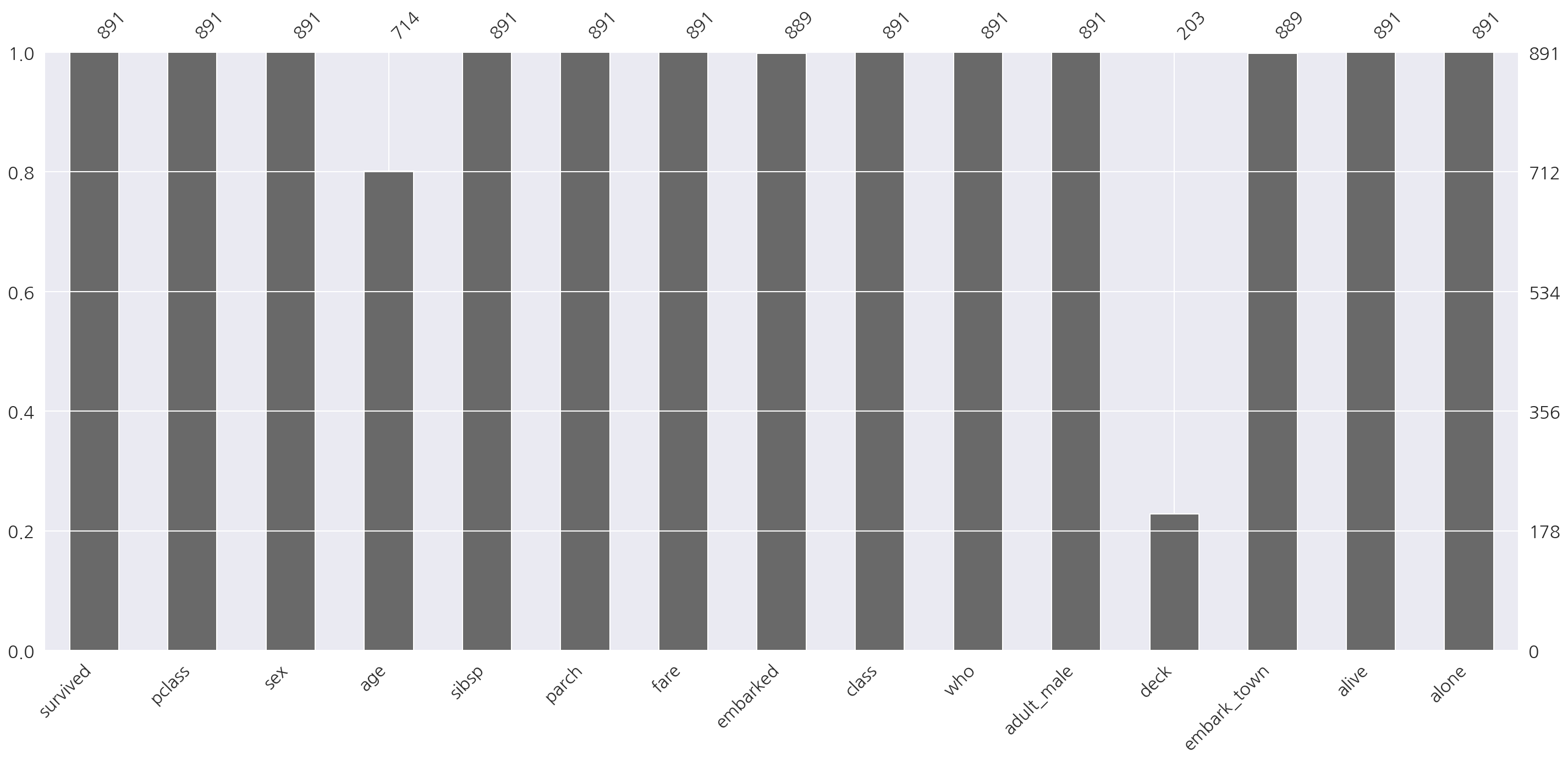
- titanic 데이터의 경우 age, embarked, deck, embarked_town에 결측값이 존재함을 알 수 있다.
결측값 삭제
titanic = titanic.dropna(thresh=int(len(titanic) * 0.5), axis=1)
msno.matrix(titanic)
plt.show()

- titanic 데이터 각 열의 비 결측값이 절 반이상인 경우만 남겨 deck을 삭제하였다.
결측값 대체
fig, axs = plt.subplots(1,2, figsize=(15,8))
sns.countplot(titanic.embark_town, ax = axs[0])
sns.countplot(titanic.embarked, ax = axs[1])
axs[0].set_title("embark_town 데이터의 분포")
axs[1].set_title("embark 데이터의 분포")
plt.show()
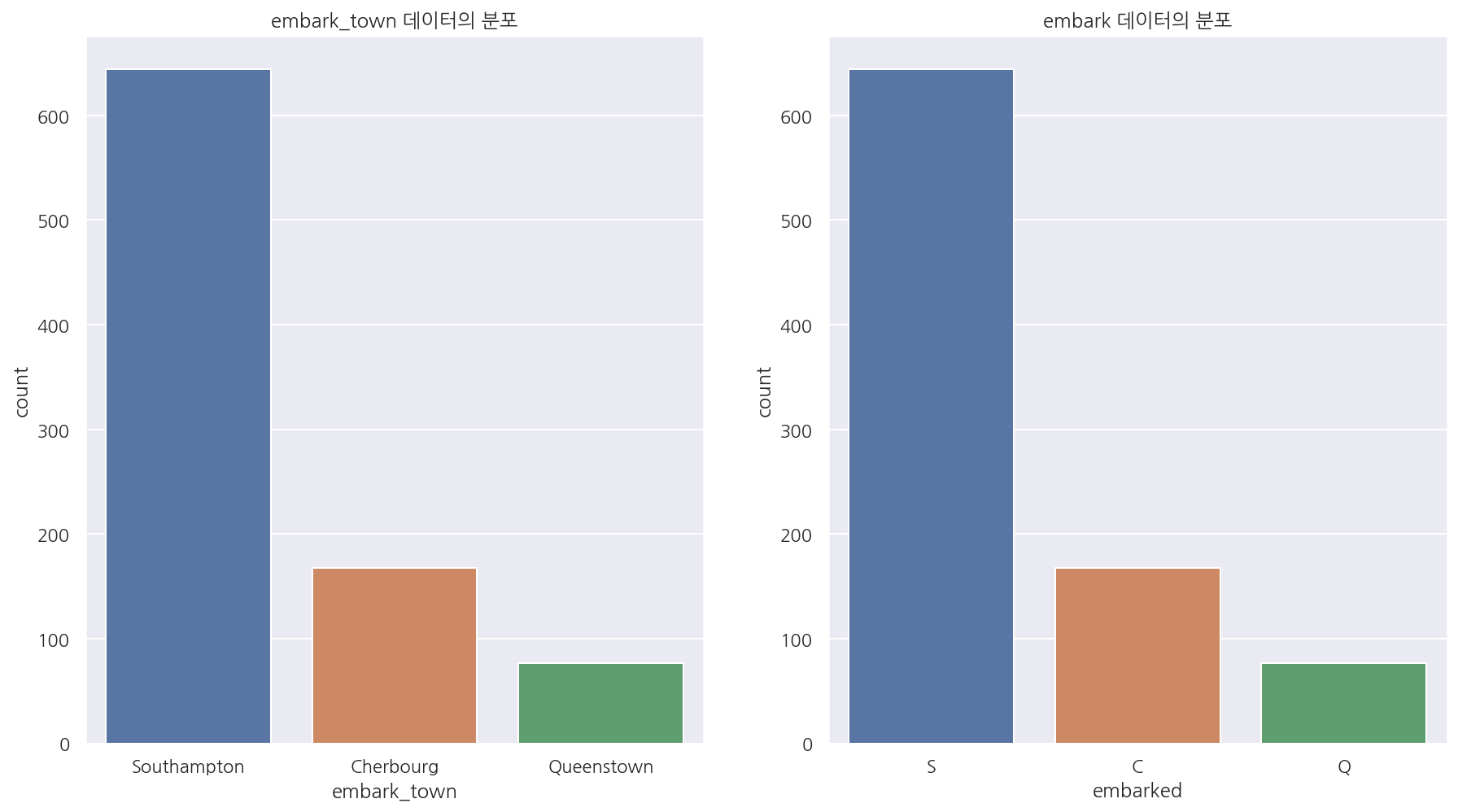
- embark_town, embark의 데이터 분포를 확인하였고 해당 데이터들의 최빈값으로 결측값을 대체 할 것이다.
imp_mode = SimpleImputer(strategy="most_frequent")
titanic["embark_town"] = imp_mode.fit_transform(titanic[["embark_town"]])
titanic["embarked"] = imp_mode.fit_transform(titanic[["embarked"]])
msno.matrix(titanic)
plt.show()
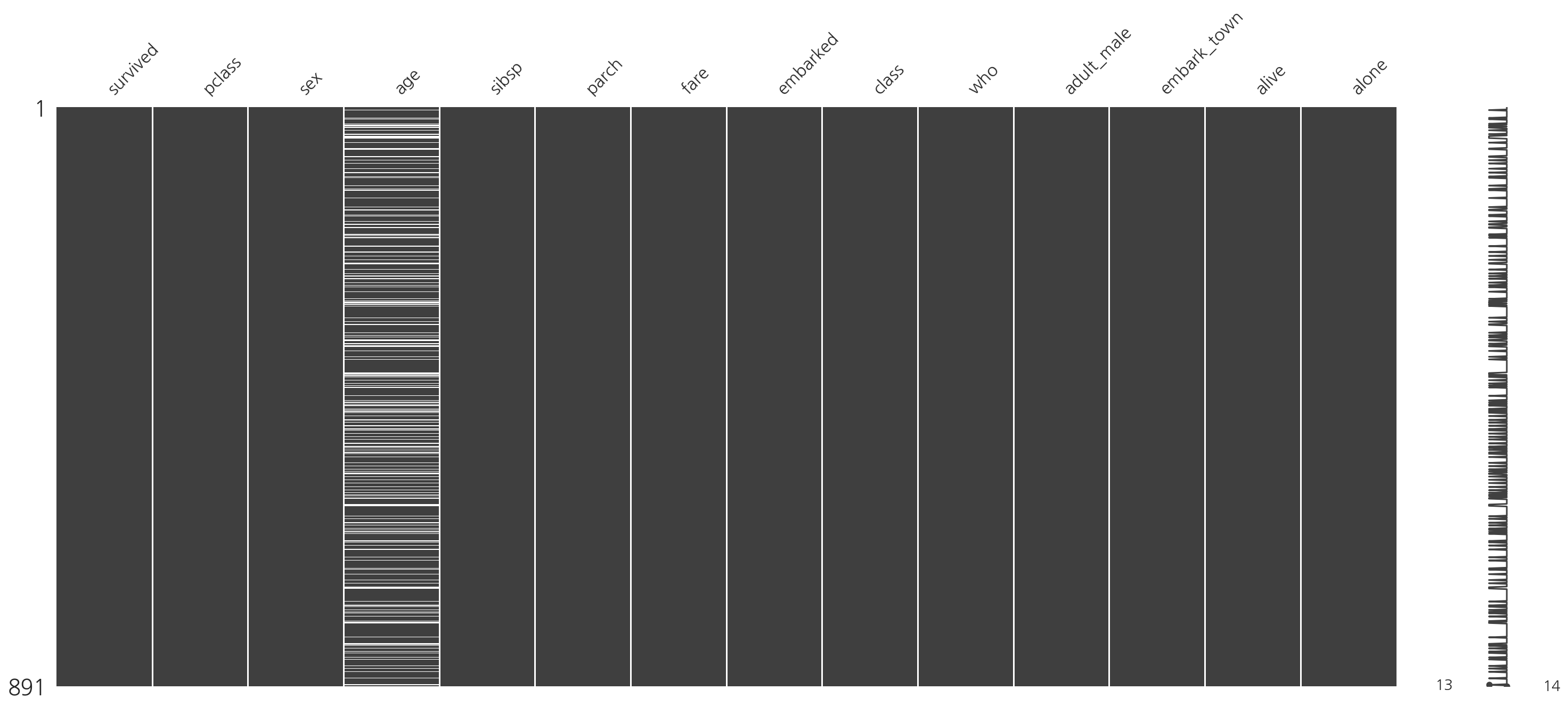
- embark_town, embark의 결측값이 사라진 것을 확인 할 수 있다.
plt.figure(figsize=(15,8))
sns.distplot(titanic.age, kde=True, color="green")
plt.title("age 데이터의 분포")
plt.show()
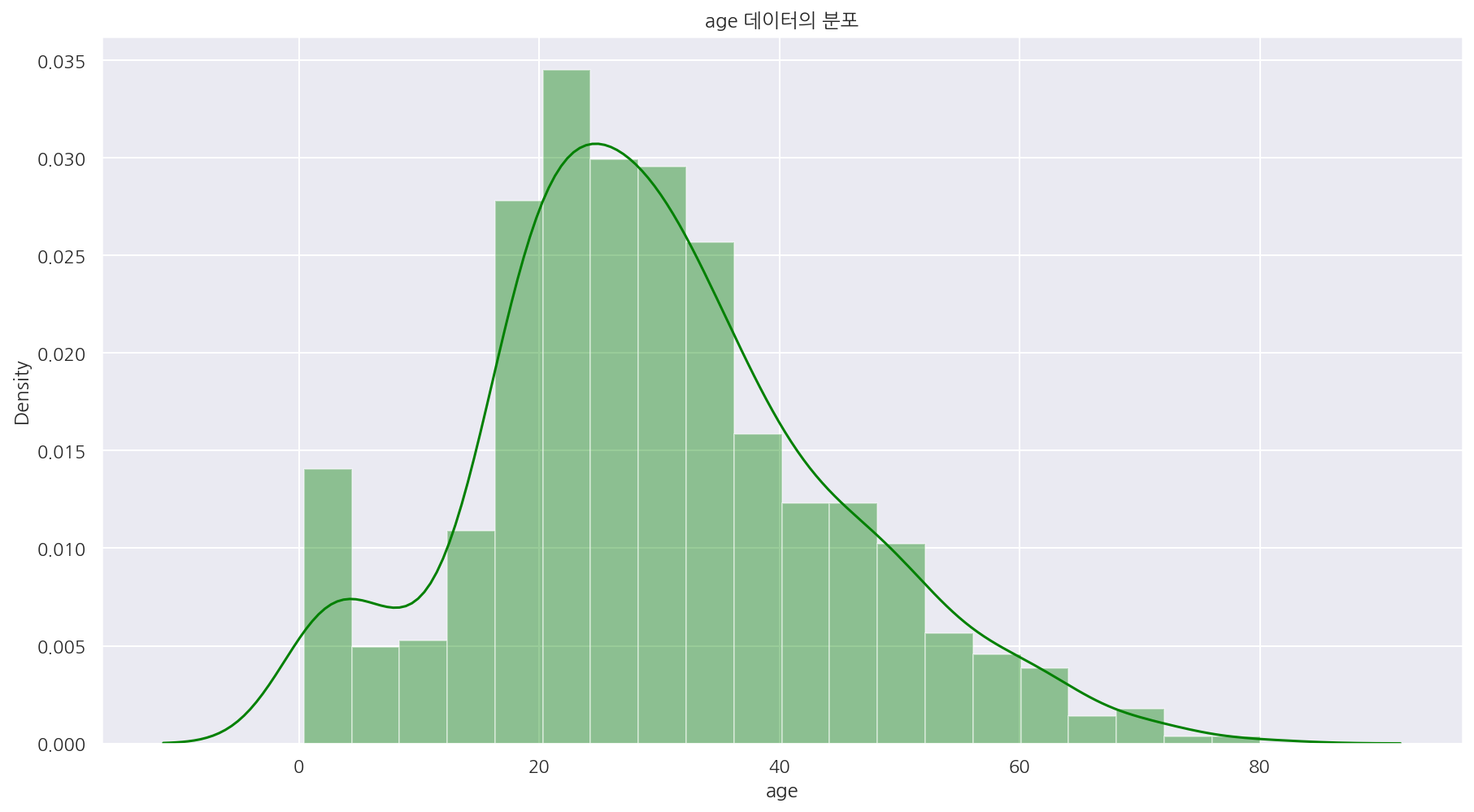
-
age의 분포를 확인하였을 때 비대칭 형태로 나옴을 확인 할 수 있다.
-
따라서 평균값보다는 중앙값으로 결측을 수정한다.
imp_median = SimpleImputer(strategy="median")
titanic["age"] = imp_median.fit_transform(titanic[["age"]])
msno.matrix(titanic)
plt.show()

- 모든 결측값이 사라진 것을 확인 할 수 있다.
2. 데이터 선택 및 스케일링
2.1 patsy 패키지
2.1.1 데이터 선택
from patsy import demo_data
df = pd.DataFrame(demo_data("x1", "x2", "x3", "x4", "x5"))
df
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 0 | 1.764052 | -0.977278 | 0.144044 | 0.333674 | -2.552990 |
| 1 | 0.400157 | 0.950088 | 1.454274 | 1.494079 | 0.653619 |
| 2 | 0.978738 | -0.151357 | 0.761038 | -0.205158 | 0.864436 |
| 3 | 2.240893 | -0.103219 | 0.121675 | 0.313068 | -0.742165 |
| 4 | 1.867558 | 0.410599 | 0.443863 | -0.854096 | 2.269755 |
patsy패키지의demo_data()를 사용하여 임의의 실수 데이터를 생성가능하다.
from patsy import dmatrix
dmatrix("x1 + x2 + x3 + 0", data = df)
DesignMatrix with shape (5, 3)
x1 x2 x3
1.76405 -0.97728 0.14404
0.40016 0.95009 1.45427
0.97874 -0.15136 0.76104
2.24089 -0.10322 0.12168
1.86756 0.41060 0.44386
Terms:
'x1' (column 0)
'x2' (column 1)
'x3' (column 2)
-
patsy패키지의dmatrix(formula, data)를 이용하여 formula에서 지정한대로 data를 변환해서 출력할 수 있다. -
전체 데이터에서 x1, x2, x3를 추출하였다.
dmatrix("x1 + x2 + x3", data = df)
DesignMatrix with shape (5, 4)
Intercept x1 x2 x3
1 1.76405 -0.97728 0.14404
1 0.40016 0.95009 1.45427
1 0.97874 -0.15136 0.76104
1 2.24089 -0.10322 0.12168
1 1.86756 0.41060 0.44386
Terms:
'Intercept' (column 0)
'x1' (column 1)
'x2' (column 2)
'x3' (column 3)
- +0 (혹은 -1) 옵션이 없으면 Intercept라는 상수열이 추가된다.
# numpy 함수
# dmatrix("x1 + np.log(np.abs(x2))", data = df)
# 사용자 정의 함수
def ten_times(x):
return 10 * x
dmatrix("ten_times(x1)", data = df)
DesignMatrix with shape (5, 2)
Intercept ten_times(x1)
1 17.64052
1 4.00157
1 9.78738
1 22.40893
1 18.67558
Terms:
'Intercept' (column 0)
'ten_times(x1)' (column 1)
- 넘파이 함수나 사용자 정의 함수 등도 사용가능하다.
# 상호작용항
# dmatrix("x1 + x2 + x1:x2 + 0", data = df)
dmatrix("x1 * x2 + 0", data = df)
DesignMatrix with shape (5, 3)
x1 x2 x1:x2
1.76405 -0.97728 -1.72397
0.40016 0.95009 0.38018
0.97874 -0.15136 -0.14814
2.24089 -0.10322 -0.23130
1.86756 0.41060 0.76682
Terms:
'x1' (column 0)
'x2' (column 1)
'x1:x2' (column 2)
:또는*을 사용하여 두 변수의 곱으로 나타나는 상호작용항을 출력할 수 있다.
dmatrix("x1 + x2 + I(x1 + x2) + 0", data = df)
DesignMatrix with shape (5, 3)
x1 x2 I(x1 + x2)
1.76405 -0.97728 0.78677
0.40016 0.95009 1.35025
0.97874 -0.15136 0.82738
2.24089 -0.10322 2.13767
1.86756 0.41060 2.27816
Terms:
'x1' (column 0)
'x2' (column 1)
'I(x1 + x2)' (column 2)
- 곱을 제외한 변수의 연산은
I()안에 기입하여 출력 가능하다.
2.1.2 데이터 스케일링
데이터 스케일링은 모든 피처(변수)들의 단위(범위 혹은 분포)를 똑같이 만들어 주는 작업이다.
데이터 스케일링은 선형 회귀 분석에서 조건수를 낮추기 위한 방법 등으로 사용한다.
dm = dmatrix("center(x1) + 0", data = df)
dm
DesignMatrix with shape (5, 1)
center(x1)
0.31377
-1.05012
-0.47154
0.79061
0.41728
Terms:
'center(x1)' (column 0)
-
center()를 이용하여 평균을 0으로 스케일링 하였다. -
이는
df.x1 - np.mean(df.x1)와 같다.
dmatrix("standardize(x1) + 0", data = df)
DesignMatrix with shape (5, 1)
standardize(x1)
0.47060
-1.57500
-0.70723
1.18578
0.62584
Terms:
'standardize(x1)' (column 0)
-
standardize()를 이용하여 평균을 0, 표준편차를 1로 스케일링 하였다. -
이는
(df.x1 - np.mean(df.x1)) / np.std(df.x1)와 같다.
dmatrix("scale(x1) + 0", data = df)
DesignMatrix with shape (5, 1)
scale(x1)
0.47060
-1.57500
-0.70723
1.18578
0.62584
Terms:
'scale(x1)' (column 0)
scale()은standardize()와 같은 결과이다.
2.2 sklearn.preprocessing 패키지
X = np.arange(7).reshape(-1, 1)
X
array([[0],
[1],
[2],
[3],
[4],
[5],
[6]])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X)
scaler.transform(X)
array([[-1.5],
[-1. ],
[-0.5],
[ 0. ],
[ 0.5],
[ 1. ],
[ 1.5]])
-
sklearn의 서브 패키지preprocessing의StandardScaler()를 이용하여 평균을 0, 표준편차를 1로 스케일링 하였다. -
sklearn의 스케일링 작업은fit(),trasnform()의 과정으로 이루어진다. -
이를 줄여서
fit_transform()으로 사용하여도 된다. -
주의할 점은 입력하는 원본 데이터는 반드시 2차원 배열이어야한다.
# Outlier 추가
X2 = np.vstack([X, [[1000]]])
X2
array([[ 0],
[ 1],
[ 2],
[ 3],
[ 4],
[ 5],
[ 6],
[1000]])
from sklearn.preprocessing import RobustScaler
scaler = RobustScaler()
scaler.fit_transform(X2)
array([[-1.00000000e+00],
[-7.14285714e-01],
[-4.28571429e-01],
[-1.42857143e-01],
[ 1.42857143e-01],
[ 4.28571429e-01],
[ 7.14285714e-01],
[ 2.84714286e+02]])
-
sklearn.preprocessing의RobustScaler()를 이용하여 중앙값을 0, IQR을 1로 스케일링 하였다. -
이상값이 있는 경우
RobustScaler()를 사용한다.
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree = 2, include_bias = True)
poly.fit_transform(X)
array([[ 1., 0., 0.],
[ 1., 1., 1.],
[ 1., 2., 4.],
[ 1., 3., 9.],
[ 1., 4., 16.],
[ 1., 5., 25.],
[ 1., 6., 36.]])
sklearn.preprocessing의PolynomialFeatures()를 이용하면 다항식을 만들 수 있다.
- degree는 차수 ,include_bias는 상수항 생성 여부 옵션으로 디폴트는 각각 2, True이다.
X = np.arange(9).reshape(-1, 1)
X
array([[0],
[1],
[2],
[3],
[4],
[5],
[6],
[7],
[8]])
from sklearn.preprocessing import FunctionTransformer
def Square(X):
x = X
y = X**2
X_new = np.hstack([x, y])
return X_new
func_trans = FunctionTransformer(Square)
X2 = func_trans.fit_transform(X)
X2
array([[ 0, 0],
[ 1, 1],
[ 2, 4],
[ 3, 9],
[ 4, 16],
[ 5, 25],
[ 6, 36],
[ 7, 49],
[ 8, 64]])
sklearn.preprocessing의FunctionTransformer()를 이용하면 함수식을 만들 수 있다.
- 위 예시에선 $X$와 $X^2$ 값을 출력하였다.
plt.figure(figsize=(15,8))
plt.plot(X2[:,0], X2[:,1], "ro--")
plt.show()
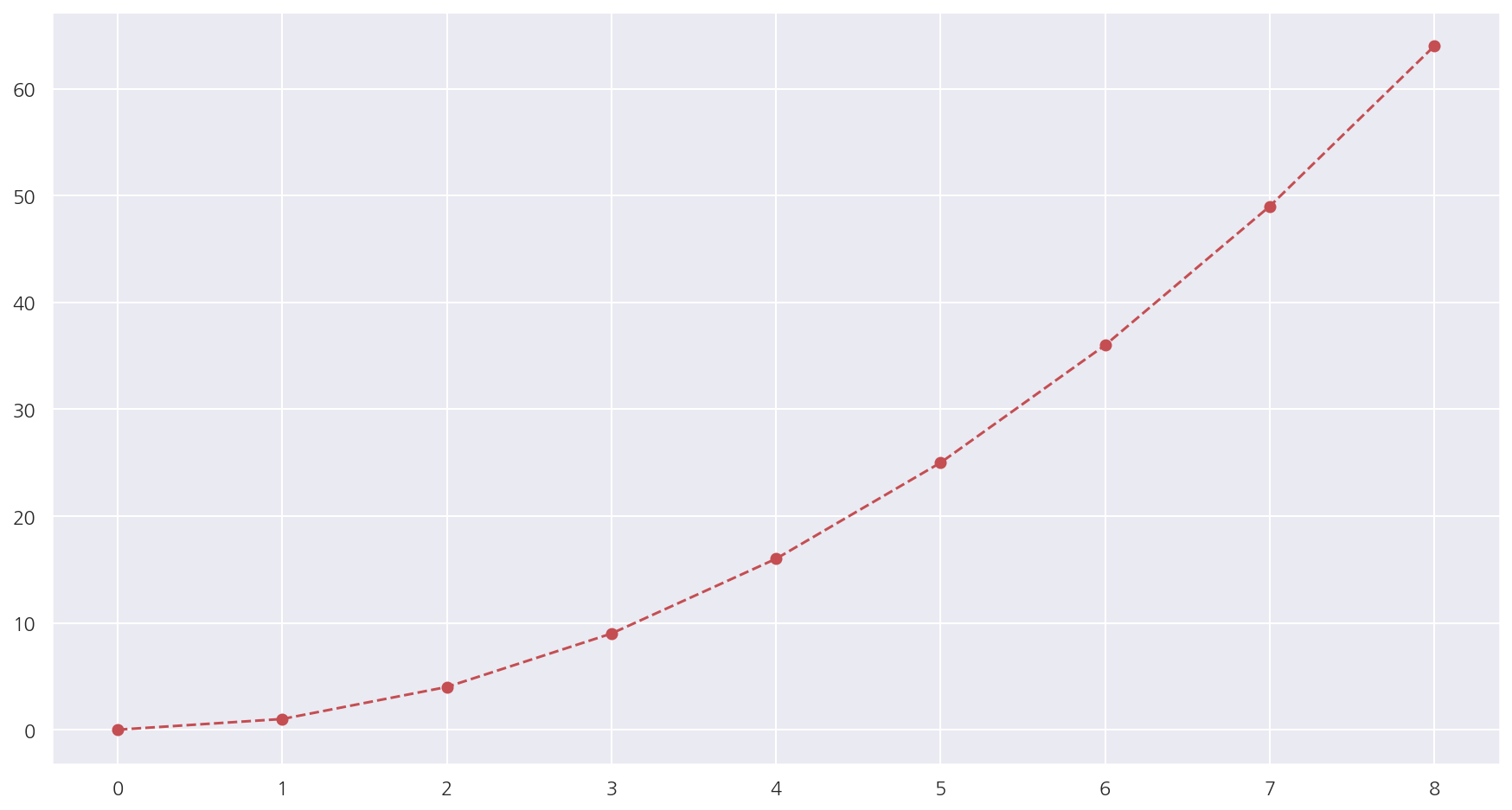
- 그림으로 잘 변환된 것을 확인 할 수 있다.
3. 범주형 데이터 처리
3.1 풀랭크(Full-Rank)
df1 = pd.DataFrame(["A", "B", "AB", "O"], columns=["x"])
df1
| x | |
|---|---|
| 0 | A |
| 1 | B |
| 2 | AB |
| 3 | O |
dmatrix("x + 0", data = df1)
DesignMatrix with shape (4, 4)
x[A] x[AB] x[B] x[O]
1 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
Terms:
'x' (columns 0:4)
-
혈액형 X가 A일 때 1,0,0,0
혈액형 x가 B일 때 0,0,1,0 등으로 출력되는 것을 확인 할 수 있다.
df3 = pd.DataFrame([1, 2, 3, 4], columns=["x"])
df3
| x | |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
dmatrix("C(x) + 0", data = df3)
DesignMatrix with shape (4, 4)
C(x)[1] C(x)[2] C(x)[3] C(x)[4]
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Terms:
'C(x)' (columns 0:4)
- 정수로 된 범주형 데이터의 경우
C()를 사용한다.
dm = dmatrix("C(x, levels=['A', 'B', 'AB', 'O']) + 0", data = df1)
dm
DesignMatrix with shape (4, 4)
Columns:
["C(x, levels=['A', 'B', 'AB', 'O'])[A]",
"C(x, levels=['A', 'B', 'AB', 'O'])[B]",
"C(x, levels=['A', 'B', 'AB', 'O'])[AB]",
"C(x, levels=['A', 'B', 'AB', 'O'])[O]"]
Terms:
"C(x, levels=['A', 'B', 'AB', 'O'])" (columns 0:4)
(to view full data, use np.asarray(this_obj))
np.asarray(dm)
array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
C()안에 levels 옵션을 사용하여 각 범주값이 대응하는 더미변수의 순서도 바꿀 수 있다.
3.2 축소랭크(reduce-rank)
dmatrix("x", data = df1)
DesignMatrix with shape (4, 4)
Intercept x[T.AB] x[T.B] x[T.O]
1 0 0 0
1 0 1 0
1 1 0 0
1 0 0 1
Terms:
'Intercept' (column 0)
'x' (columns 1:4)
- 축소랭크 방식에선 특정한 하나의 범주값을 기준으로 하여 기준값에 대응하는 더미변수 값은 모두 1로서 Intercpet로 설정한다.
dmatrix("C(x, Treatment('B'))", data = df1)
DesignMatrix with shape (4, 4)
Columns:
['Intercept',
"C(x, Treatment('B'))[T.A]",
"C(x, Treatment('B'))[T.AB]",
"C(x, Treatment('B'))[T.O]"]
Terms:
'Intercept' (column 0), "C(x, Treatment('B'))" (columns 1:4)
(to view full data, use np.asarray(this_obj))
C()안에Treatment()를 사용하여 기준이 대는 범주값을 바꿀 수 있다.
3.3 두 개의 범주형 변수
3.3.1 통합 축소형 방식
df4 = pd.DataFrame([["A", "X"], ["B", "X"], ["A", "Y"], ["B", "Y"]], columns=["x1", "x2"])
df4
| x1 | x2 | |
|---|---|---|
| 0 | A | X |
| 1 | B | X |
| 2 | A | Y |
| 3 | B | Y |
dmatrix("x1 + x2", data = df4)
DesignMatrix with shape (4, 3)
Intercept x1[T.B] x2[T.Y]
1 0 0
1 1 0
1 0 1
1 1 1
Terms:
'Intercept' (column 0)
'x1' (column 1)
'x2' (column 2)
- x1과 x2가 각각 축소된 것을 확인 할 수 있다.
dmatrix("x1 + x2 + 0", data = df4)
DesignMatrix with shape (4, 3)
x1[A] x1[B] x2[T.Y]
1 0 0
0 1 0
1 0 1
0 1 1
Terms:
'x1' (columns 0:2)
'x2' (column 2)
- x2만 축소된 것을 확인 할 수 있다.
3.3.2 상호작용 방식
dmatrix("x1:x2 + 0", data = df4)
DesignMatrix with shape (4, 4)
x1[A]:x2[X] x1[B]:x2[X] x1[A]:x2[Y] x1[B]:x2[Y]
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Terms:
'x1:x2' (columns 0:4)
- 두 범주형 변수의 경우의 수를 갖는 새로운 범주형 변수의 풀랭크 방식으로 결과를 출력한다.

Leave a comment