[Python] 모두의 딥러닝 - 03. 신경망의 이해[퍼셉트론]
Updated:
모두의 딥러닝 교재를 토대로 공부한 내용입니다.
실습과정에서 필요에 따라 코드나 이론에 대한 추가, 수정사항이 있습니다.
기본 세팅
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
mpl.rc('font', family='NanumGothic') # 폰트 설정
mpl.rc('axes', unicode_minus=False) # 유니코드에서 음수 부호 설정
# 차트 스타일 설정
sns.set(font="NanumGothic", rc={"axes.unicode_minus":False}, style='darkgrid')
plt.rc("figure", figsize=(10,8))
warnings.filterwarnings("ignore")
6. 퍼셉트론
퍼셉트론은 신경망을 이루는 가장 중요한 기본 단위이다.
인간의 뇌에 존재하는 뉴런의 역할로 입력 값과 활성화 함수를 사용해 출력 값을 다음으로 넘긴다.
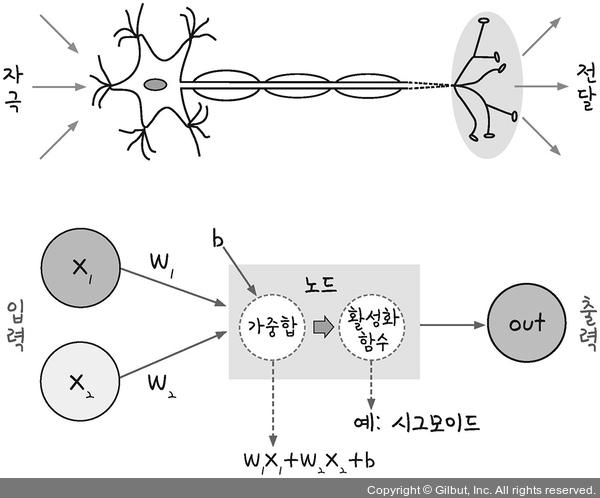
출처: https://thebook.io/080228/part03/ch06-01/
6.1 퍼셉트론 과정
입력 값 $x$에 가중치(Weight) $w$를 적용한 후 더한다. $\rightarrow \sum_{i} w_{i}x_{i}$
편향(bias) $b$를 더해 가중합을 계산한다. $\rightarrow \sum_{i} w_{i}x_{i} + b$
가중합의 결과를 놓고 1 또는 0을 출력해서 다음으로 전달한다.
1 또는 0을 출력하는 판단은 활성화 함수 $\sigma$로 결정한다. $\rightarrow \sigma(\sum_{i} w_{i}x_{i} + b)$
대표적인 활성화 함수로는 시그모이드 함수가 있다.
6.2 게이트
컴퓨터는 두 가지의 디지털 값, 0과 1을 입력해 하나의 값을 출력하는 회로가 모여 만들어진다.
이 회로를 게이트(Gate)라고 한다.
게이트의 대표적인 유형은 다음과 같다.
-
AND: 두 입력이 모두 1일 때 1을 출력하는 게이트
-
OR: 두 입력 중 하나라도 1이면 1을 출력하는 게이트
-
NOT: 입력이 1이면 0, 입력이 0이면 1을 출력하는 게이트
-
NAND: AND와 반대로 두 입력이 모두 1일 때 0을 출력하는 게이트
-
NOR: OR과 반대로 두 입력 중 하나라도 1이면 0을 출력하는 게이트
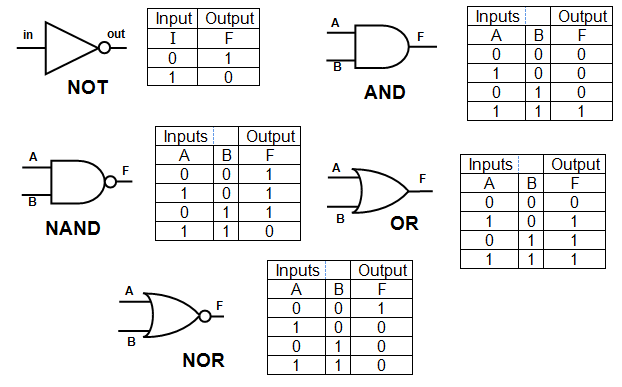
출처: http://www.schoolphysics.co.uk/age14-16/Electronics/text/Logic_gates/index.html
6.3 XOR 문제
앞서 확인한 게이트들은 모두 퍼셉트론으로 구현 가능하다.
하지만 XOR게이트는 퍼셉트론으로 해결할 수 없다.
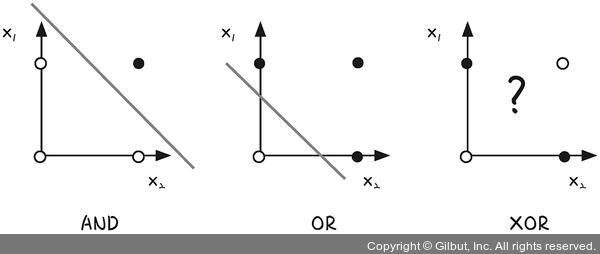
출처: https://thebook.io/080228/part03/ch06/03-01/
위 그림에서 AND 게이트와 OR 게이트는 직선 하나로 흰점(0)과 검은점(1) 구분이 가능하다.
반면 XOR 게이트는 어떤 직선이던 하나로는 점을 구분할 수 없다.
- XOR: 서로 다른 두 값이 입력되면 1을 반환하는 게이트
7. 다층 퍼셉트론
다음 그림을 보면 종이를 반으로 접었을 때 직선 하나로 점을 구분할 수 있다.
즉, 좌표 평면 자체에 변화를 주면 XOR 문제를 해결할 수 있다.
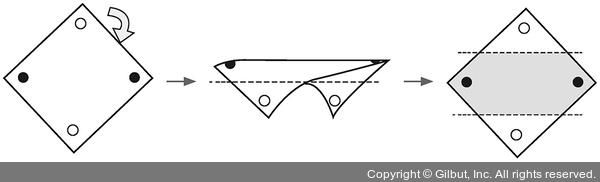
출처: https://thebook.io/080228/part03/ch07-01/
평면에 변화를 주면서 직선까지 찾으려면 두 개의 퍼셉트론을 한번에 계산할 수 있어야 하며,
이를 가능하게 하기 위해 숨어있는 층, 은닉층(hidden layer)를 만든다.
입력층에서 출력층으로 가기 전에 은닉층에서 평면을 왜곡하는 것이다.
7.1 다층 퍼셉트론의 설계
다음 그림은 은닉층을 포함한 다층 퍼셉트론 구조이다.
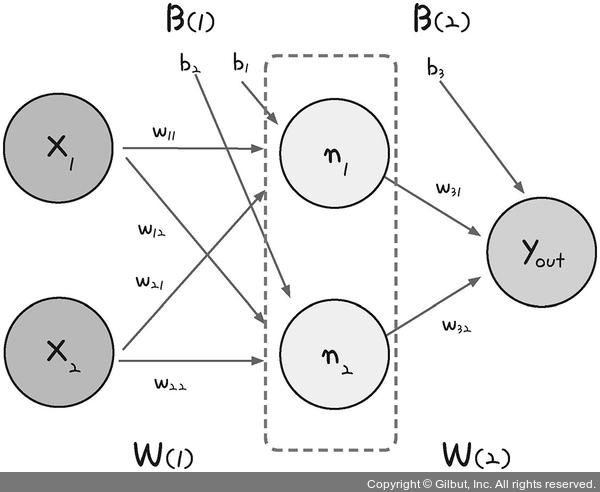
출처: https://thebook.io/080228/part03/ch07/01/
다층 퍼셉트론의 과정을 세분화해서 살펴보자.
(교재에서 활성화 함수($\sigma$)는 두번 모두 시그모이드 함수를 사용한다.)
[입력층]
값에 가중치($w$)와 바이어스($b$)를 적용 후 활성화 함수($\sigma$)를 적용해 은닉층에 보낸다.
-
$x_{1}$
-
$x_{2}$
[은닉층]
중간 정거장으로 노드(node)라고 하며 은닉층의 값은 다시 같은 과정으로 출력층에 전달된다.
-
$n_{1} = \sigma (x_{1} w_{11} + x_{2} w_{21} + b_{1})$
-
$n_{2} = \sigma (x_{1} w_{12} + x_{2} w_{22} + b_{2})$
[출력층]
최종 출력값
- $y_{out} = \sigma (n_{1} w_{31} + n_{2} w_{32} + b_{3})$
7.2 XOR 해결
이제 다층 퍼셉트론을 이용해서 XOR 문제를 해결해보자.
앞서 확인한 구조에 따라 다음과 같은 가중치와 바이어스에 대한 배열이 필요하다.
\[W(1) = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \\ \end{bmatrix} , \quad B(1) = \begin{bmatrix} b_{1} \\ b_{2} \end{bmatrix}\] \[W(2) = \begin{bmatrix} w_{31} \\ w_{32} \end{bmatrix} , \quad B(2) = \begin{bmatrix} b_{3} \end{bmatrix}\]다만 XOR 문제를 해결하는 가중치와 바이어스 조합은 무수히 많다.
여기선 임의로 한 조합을 선택해서 실습할 것이다.
# 가중치, 바이어스
W_1 = np.array([[-2,2],
[-2,2]])
W_2 = np.array([1,1])
B_1 = np.array([3,-1])
B_2 = np.array(-1)
- 가중치와 바이어스는 임의로 한 조합을 선택해서 설정하였다.
# 퍼셉트론
def MLP(x, w, b):
y = np.sum(w*x) + b
if y <= 0:
return 0
else:
return 1
-
퍼셉트론 함수를 설정하였다.
-
가중합이 0보다 작거나 같으면 0, 그렇지 않으면 1로 출력한다.
-
즉, 활성화 함수는 여기선 항등함수를 사용한 듯 하며 임계값을 0으로 설정하였다.
# NAND 게이트 (은닉층 첫 번째 값 생성하는 가중치, 바이어스 적용)
def NAND(x1,x2):
n1 = MLP(np.array([x1,x2]), W_1[:,0], B_1[0])
return n1
# 출력 값 확인
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = NAND(x[0], x[1])
print(f"입력 값: {x} 출력 값: {y}")
입력 값: (0, 0) 출력 값: 1
입력 값: (1, 0) 출력 값: 1
입력 값: (0, 1) 출력 값: 1
입력 값: (1, 1) 출력 값: 0
-
가중합에 퍼셉트론 함수를 적용하여 NAND 게이트 결과가 출력되었다.
-
즉, 은닉층의 $n_{1}$은 NAND 게이트에 따른 결과를 사용한다.
# OR 게이트 (은닉층 두 번째 값 생성하는 가중치, 바이어스 적용)
def OR(x1,x2):
n2 = MLP(np.array([x1,x2]), W_1[:,1], B_1[1])
return n2
# 출력 값 확인
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = OR(x[0], x[1])
print(f"입력 값: {x} 출력 값: {y}")
입력 값: (0, 0) 출력 값: 0
입력 값: (1, 0) 출력 값: 1
입력 값: (0, 1) 출력 값: 1
입력 값: (1, 1) 출력 값: 1
-
가중합에 퍼셉트론 함수를 적용하니 OR 게이트 결과가 출력되었다.
-
즉, 은닉층의 $n_{2}$는 OR 게이트에 따른 결과를 사용한다.
# AND 게이트 (출력 값을 생성하는 가중치, 바이어스 적용)
def AND(x1,x2):
y_out = MLP(np.array([x1,x2]), W_2, B_2)
return y_out
# 출력 값 확인
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = AND(x[0], x[1])
print(f"입력 값: {x} 출력 값: {y}")
입력 값: (0, 0) 출력 값: 0
입력 값: (1, 0) 출력 값: 0
입력 값: (0, 1) 출력 값: 0
입력 값: (1, 1) 출력 값: 1
- 출력층의 $y_{out}$는 AND 게이트에 따른 결과를 사용한다.
# XOR 게이트
def XOR(x1,x2):
return AND(NAND(x1,x2), OR(x1,x2))
# 출력 값 확인
for x in [(0, 0), (1, 0), (0, 1), (1, 1)]:
y = XOR(x[0], x[1])
print(f"입력 값: {x} 출력 값: {y}")
입력 값: (0, 0) 출력 값: 0
입력 값: (1, 0) 출력 값: 1
입력 값: (0, 1) 출력 값: 1
입력 값: (1, 1) 출력 값: 0
-
서로 다른 두 값이 입력된 경우에만 1이 출력됨을 알 수 있다.
-
즉, XOR 게이트는 NAND와 OR 게이트의 결과에 AND 게이트를 적용하여 해결 가능하다.

Leave a comment