[Python] 데이터 사이언스 스쿨 - 5.3 다중공선성과 변수선택
Updated:
데이터 사이언스 스쿨 자료를 토대로 공부한 내용입니다.
실습과정에서 필요에 따라 내용의 누락 및 추가, 수정사항이 있습니다.
기본 세팅
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
mpl.rc('font', family='NanumGothic') # 폰트 설정
mpl.rc('axes', unicode_minus=False) # 유니코드에서 음수 부호 설정
# 차트 스타일 설정
sns.set(font="NanumGothic", rc={"axes.unicode_minus":False}, style='darkgrid')
plt.rc("figure", figsize=(10,8))
warnings.filterwarnings("ignore")
5.3 다중공선성과 변수선택
다중공선성: 독립 변수의 일부가 다른 독립 변수의 조합으로 표현될 수 있는 경우로서 즉, 선형 독립이 아닌 경우이다.
이는 독립 변수의 공분산 행렬이 full rank 이어야 한다는 조건을 침해한다.
예제 데이터
from statsmodels.datasets.longley import load_pandas
dfy = load_pandas().endog # 종속변수 이름: TOTEMP
dfX = load_pandas().exog
df = pd.concat([dfy, dfX], axis=1)
corr_M = dfX.corr() # 독립변수 상관관계
mask = np.array(corr_M)
mask[np.tril_indices_from(mask)] = False
plt.figure(figsize= (10,8))
sns.heatmap(corr_M,
cmap = sns.light_palette("red", as_cmap=True),
annot = True,
mask = mask)
plt.show()
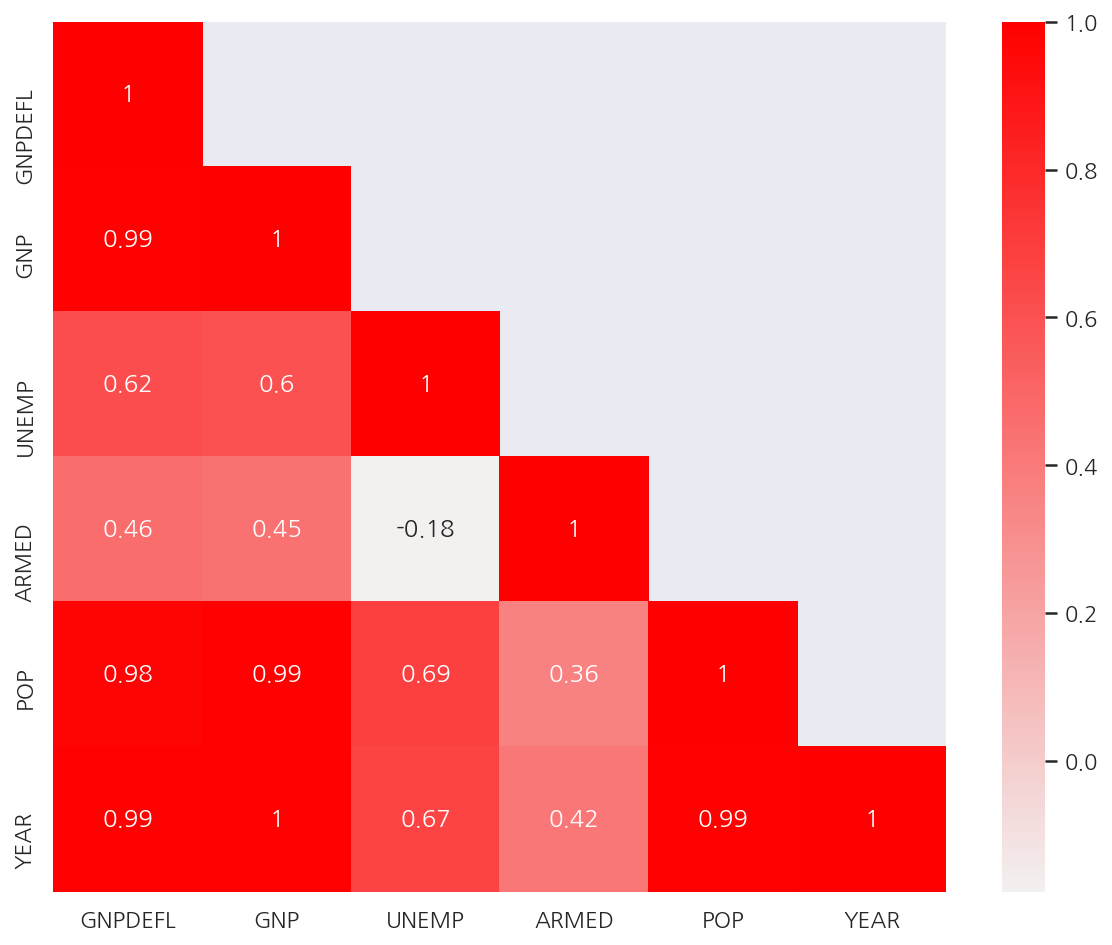
- 독립변수간의 상관관계가 강한 경우가 많다. 즉, 다중공선성이 존재한다.
5.3.1 다중공선성 문제점: 조건수 증가
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
def get_model1(seed):
df_train, df_test = train_test_split(df, test_size=0.5, random_state=seed)
model = sm.OLS.from_formula("TOTEMP ~ GNPDEFL + POP + GNP + YEAR + ARMED + UNEMP", data=df_train)
return df_train, df_test, model.fit()
df_train, df_test, result1 = get_model1(3)
print(result1.summary())
OLS Regression Results
==============================================================================
Dep. Variable: TOTEMP R-squared: 1.000
Model: OLS Adj. R-squared: 0.997
Method: Least Squares F-statistic: 437.5
Date: Sat, 12 Jun 2021 Prob (F-statistic): 0.0366
Time: 01:03:49 Log-Likelihood: -44.199
No. Observations: 8 AIC: 102.4
Df Residuals: 1 BIC: 103.0
Df Model: 6
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -1.235e+07 2.97e+06 -4.165 0.150 -5e+07 2.53e+07
GNPDEFL 106.2620 75.709 1.404 0.394 -855.708 1068.232
POP 2.2959 0.725 3.167 0.195 -6.915 11.506
GNP -0.3997 0.120 -3.339 0.185 -1.920 1.121
YEAR 6300.6231 1498.900 4.203 0.149 -1.27e+04 2.53e+04
ARMED -0.2450 0.402 -0.609 0.652 -5.354 4.864
UNEMP -6.3311 1.324 -4.782 0.131 -23.153 10.491
==============================================================================
Omnibus: 0.258 Durbin-Watson: 1.713
Prob(Omnibus): 0.879 Jarque-Bera (JB): 0.304
Skew: 0.300 Prob(JB): 0.859
Kurtosis: 2.258 Cond. No. 2.01e+10
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.01e+10. This might indicate that there are
strong multicollinearity or other numerical problems.
-
위 회귀분석 결과에서 알 수 있듯이 다중공선성이 존재시 조건수도 많아지게 된다.
-
여기서 train으로 학습한 회귀모형의 결정계수가 1로서 100%로 나타났다.
5.3.2 다중공선성 문제점: 과최적화
from sklearn.metrics import r2_score
test1 = []
for i in range(10):
df_train, df_test, result = get_model1(i)
pred_test = result.predict(df_test)
rsquared = r2_score(df_test.TOTEMP, pred_test)
test1.append(round(rsquared,3))
test1
[0.982, 0.974, 0.988, 0.759, 0.981, 0.894, 0.88, 0.931, 0.861, 0.968]
-
train에선 결정계수가 1이 었으나 test에선 모두 train보다 결정계수가 작게 나왔다.
-
원래 test에서의 예측 성능이 보통 train보다 낮긴 하지만 과최적화 문제가 있다면 성능이 더 크게 저하된다.
5.3.3 다중공선성 해결법
-
변수 선택법으로 의존적인 변수 삭제
-
PCA(principal component analysis) 방법으로 의존적인 성분 삭제
-
정규화(regularized) 방법 사용 (여기선 정규화라고 칭했지만 보통 규제라고 표현한다.)
5.3.4 분산팽창계수(VIF)
다중 공선성을 없애는 가장 기본적인 방법은 다른 독립변수에 의존하는 변수를 없애는 것이다.
가장 의존적인 독립변수를 선택하는 방법으로는 VIF(Variance Inflation Factor)를 사용할 수 있다.
-
VIF는 특정 독립변수를 나머지 독립변수로 적합했을 때 성능을 나타낸 것이다.
-
다른 변수에 의존할수록 VIF 값이 높다.
statsmodels.stats.outliers_influence의 variance_inflation_factor()를 이용하여 VIF를 계산할 수 있다.
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = pd.DataFrame()
lst = []
# 독립변수의 갯수 만큼 반복
for i in range(dfX.shape[1]):
v = variance_inflation_factor(dfX.values, i) # 컬럼을 정수로 지정한다.
lst.append(v)
vif["VIF Factor"] = lst
vif["features"] = dfX.columns
vif
| VIF Factor | features | |
|---|---|---|
| 0 | 12425.514335 | GNPDEFL |
| 1 | 10290.435437 | GNP |
| 2 | 136.224354 | UNEMP |
| 3 | 39.983386 | ARMED |
| 4 | 101193.161993 | POP |
| 5 | 84709.950443 | YEAR |
-
각 독립변수의 VIF 계수를 확인하였다.
-
이 중에서 VIF 계수가 작은 순으로 3가지 독립변수 GNP, ARMED, UNEMP만 사용해보자.
def get_model2(seed):
df_train, df_test = train_test_split(df, test_size=0.5, random_state=seed)
model = sm.OLS.from_formula("TOTEMP ~ GNP + ARMED + UNEMP", data=df_train)
return df_train, df_test, model.fit()
df_train, df_test, result2 = get_model2(3)
print(result2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: TOTEMP R-squared: 0.989
Model: OLS Adj. R-squared: 0.981
Method: Least Squares F-statistic: 118.6
Date: Sat, 12 Jun 2021 Prob (F-statistic): 0.000231
Time: 01:03:49 Log-Likelihood: -57.695
No. Observations: 8 AIC: 123.4
Df Residuals: 4 BIC: 123.7
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 5.399e+04 1013.271 53.281 0.000 5.12e+04 5.68e+04
GNP 0.0500 0.005 10.669 0.000 0.037 0.063
ARMED -1.2804 0.497 -2.574 0.062 -2.662 0.101
UNEMP -1.4265 0.363 -3.931 0.017 -2.434 -0.419
==============================================================================
Omnibus: 0.628 Durbin-Watson: 2.032
Prob(Omnibus): 0.731 Jarque-Bera (JB): 0.565
Skew: 0.390 Prob(JB): 0.754
Kurtosis: 1.958 Cond. No. 2.44e+06
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.44e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
- VIF계수가 작은 GNP, ARMED, UNEMP만을 사용하였을 때 여전히 조건수가 많지만 이전보다 줄어든 것을 알 수 있다.
df_train.std()
TOTEMP 3325.272051
GNPDEFL 10.975224
GNP 92714.595875
UNEMP 1028.961751
ARMED 678.062523
POP 6499.246792
YEAR 4.566962
dtype: float64
- 변수별 단위차가 있어 스케일링이 필요하다.
def get_model3(seed):
df_train, df_test = train_test_split(df, test_size=0.5, random_state=seed)
model = sm.OLS.from_formula("TOTEMP ~ scale(GNP) + scale(ARMED) + scale(UNEMP)", data=df_train)
return df_train, df_test, model.fit()
df_train, df_test, result3 = get_model3(3)
print(result3.summary())
OLS Regression Results
==============================================================================
Dep. Variable: TOTEMP R-squared: 0.989
Model: OLS Adj. R-squared: 0.981
Method: Least Squares F-statistic: 118.6
Date: Sat, 12 Jun 2021 Prob (F-statistic): 0.000231
Time: 01:03:49 Log-Likelihood: -57.695
No. Observations: 8 AIC: 123.4
Df Residuals: 4 BIC: 123.7
Df Model: 3
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
Intercept 6.538e+04 163.988 398.686 0.000 6.49e+04 6.58e+04
scale(GNP) 4338.7051 406.683 10.669 0.000 3209.571 5467.839
scale(ARMED) -812.1407 315.538 -2.574 0.062 -1688.215 63.933
scale(UNEMP) -1373.0426 349.316 -3.931 0.017 -2342.898 -403.187
==============================================================================
Omnibus: 0.628 Durbin-Watson: 2.032
Prob(Omnibus): 0.731 Jarque-Bera (JB): 0.565
Skew: 0.390 Prob(JB): 0.754
Kurtosis: 1.958 Cond. No. 4.77
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
-
스케일링으로 인해 조건수가 4.77로 크게 감소하였다.
-
여기서는 train으로 학습한 회귀모형의 결정계수가 0.989로 나타났다.
from sklearn.metrics import r2_score
test2 = []
for i in range(10):
df_train, df_test, result = get_model3(i)
pred_test = result.predict(df_test)
rsquared = r2_score(df_test.TOTEMP, pred_test)
test2.append(round(rsquared,3))
test2
[0.976, 0.984, 0.969, 0.94, 0.977, 0.956, 0.98, 0.992, 0.984, 0.979]
- train에서의 결정계수 0.989와 test 결정계수가 어느정도 비슷하게 나타나 이전보다 차이가 줄었다.
plt.subplot(121)
plt.plot(test1, 'ro', label="검증 성능")
plt.axhline(result1.rsquared, label="학습 성능")
plt.legend()
plt.xlabel("시드값")
plt.ylabel("성능(결정계수)")
plt.title("다중공선성 제거 전")
plt.ylim(0.7, 1.1)
plt.subplot(122)
plt.plot(test2, 'ro', label="검증 성능")
plt.axhline(result2.rsquared, label="학습 성능")
plt.legend()
plt.xlabel("시드값")
plt.ylabel("성능(결정계수)")
plt.title("다중공선성 제거 후")
plt.ylim(0.7, 1.1)
plt.suptitle("다중공선성 제거 전과 제거 후의 성능 비교", y=1.04)
plt.tight_layout()
plt.show()
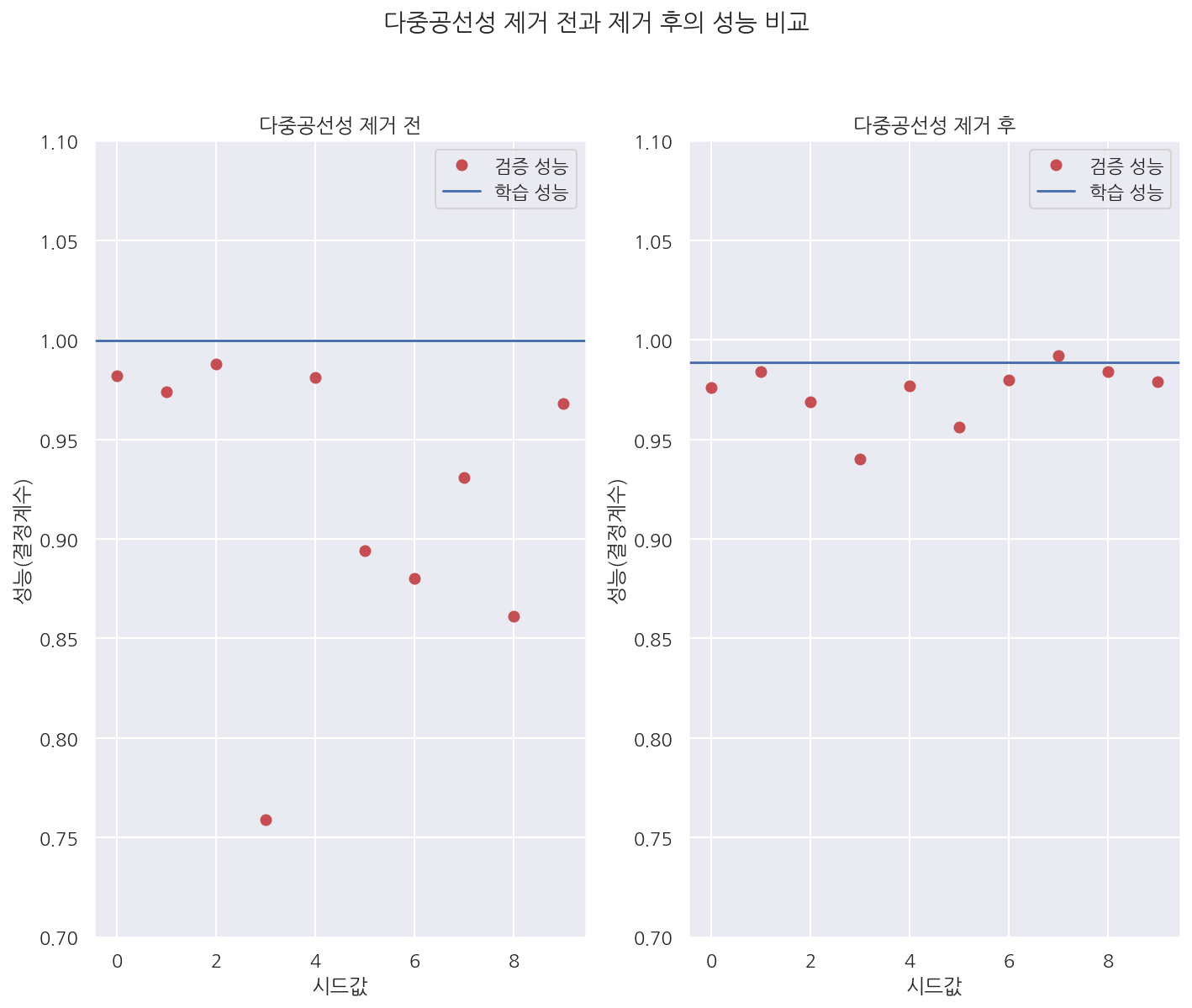
- 그래프로 확인하면 다중공선성 제거 전에는 검증/학습 성능의 차이가 크지만 제거 후 성능 차이가 감소한 것을 확인 할 수 있다.

Leave a comment